
(本題18分)
已知:正數(shù)數(shù)列![]() 的通項公式
的通項公式![]()
![]()
(1)求數(shù)列![]() 的最大項;[來源:Zxxk.Com]
的最大項;[來源:Zxxk.Com]
(2)設(shè)![]() ,確定實常數(shù)
,確定實常數(shù)![]() ,使得
,使得![]() 為等比數(shù)列;
為等比數(shù)列;
(3)(理)數(shù)列![]() ,滿足
,滿足![]() ,
,![]() ,其中
,其中![]() 為第(2)小題中確定的正常數(shù),求證:對任意
為第(2)小題中確定的正常數(shù),求證:對任意![]() ,有
,有![]() 且
且![]() 或
或![]() 且
且![]() 成立.
成立.
(文)設(shè)![]() 是滿足第(2)小題的等比數(shù)列,求使不等式
是滿足第(2)小題的等比數(shù)列,求使不等式![]() 成立的最小正整數(shù)
成立的最小正整數(shù)![]() .
.
(1)4(2)![]() (3)略
(3)略
(1)![]() ,隨n的增大而減小,
,隨n的增大而減小,
∴![]() 中的最大項為
中的最大項為![]() (2’)
(2’)
(2)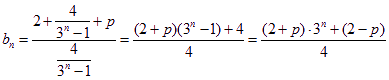 (4’)
(4’)
![]() 為等比數(shù)列
為等比數(shù)列![]()
![]()
![]()
![]()
反之當(dāng)![]() 時,
時,![]() 為等比數(shù)列;
為等比數(shù)列;![]() 時,
時,![]() 為等比數(shù)列
為等比數(shù)列
∴當(dāng)且僅當(dāng)![]() 時,
時,![]()
![]() 為等比數(shù)列(8’)
為等比數(shù)列(8’)
(3)(理)按題意![]() [來源:學(xué)+科+網(wǎng)]
[來源:學(xué)+科+網(wǎng)]
∵![]() ,
,![]() ,進(jìn)而當(dāng)
,進(jìn)而當(dāng)![]() 時,
時,![]() (10’)
(10’)
![]()
∵![]() ,∴由數(shù)學(xué)歸納法,對
,∴由數(shù)學(xué)歸納法,對![]() ,且
,且
![]()
![]() (15’)
(15’)
特別有![]()
![]()
∴![]() 且
且![]() 或
或![]()
![]() 且
且![]() (18’)
(18’)
(文)若![]() ,則
,則![]()
![]()
![]() 的
的![]() 不存在(11’)
不存在(11’)
若![]() ,則
,則![]()
![]()
![]()
![]() (16’)
(16’)
∴![]() 為偶數(shù) ∵
為偶數(shù) ∵![]()
∴當(dāng)![]() 時,
時,![]() 的最小值為8;當(dāng)
的最小值為8;當(dāng)![]() 時,滿足條件的
時,滿足條件的![]() 不存在(18’)
不存在(18’)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年福建省數(shù)學(xué)選修1-2模塊考試數(shù)學(xué)試卷(解析版) 題型:解答題
(本題18 分)已知數(shù)列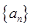 :
: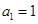 、
、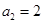 、
、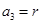 且
且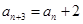 (
(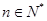 ),與數(shù)列
),與數(shù)列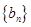 :
: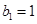 、
、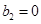 、
、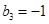 、
、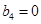 且
且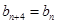 (
(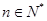 ).
).
記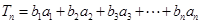 .
.
(1)若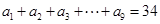 ,求
,求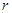 的值;
的值;
(2)求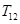 的值,并求證當(dāng)
的值,并求證當(dāng)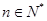 時,
時,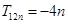 ;
;
(3)已知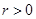 ,且存在正整數(shù)
,且存在正整數(shù)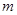 ,使得在
,使得在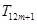 ,
,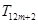 ,
, ,
,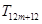 中有4項為100.求
中有4項為100.求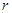 的值,并指出哪4項為100.
的值,并指出哪4項為100.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年上海市高三上學(xué)期期中考試?yán)砜茢?shù)學(xué)試卷 題型:解答題
(本題18 分)已知數(shù)列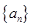 :
: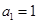 、
、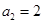 、
、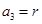 且
且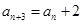 (
(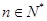 ),與數(shù)列
),與數(shù)列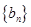 :
: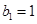 、
、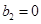 、
、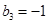 、
、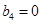 且
且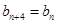 (
(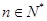 ).
).
記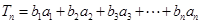 .
.
(1)若 ,求
,求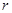 的值;
的值;
(2)求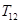 的值,并求證當(dāng)
的值,并求證當(dāng)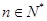 時,
時,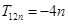 ;
;
(3)已知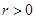 ,且存在正整數(shù)
,且存在正整數(shù)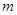 ,使得在
,使得在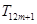 ,
,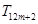 ,
, ,
,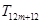 中有4項為100。求
中有4項為100。求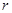 的值,并指出哪4項為100。
的值,并指出哪4項為100。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010屆上海市虹口區(qū)高三第二次模擬考試數(shù)學(xué)卷 題型:解答題
(本題18分)
已知:正數(shù)數(shù)列 的通項公式
的通項公式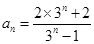

(1)求數(shù)列 的最大項;[來源:Zxxk.Com]
的最大項;[來源:Zxxk.Com]
(2)設(shè) ,確定實常數(shù)
,確定實常數(shù) ,使得
,使得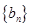 為等比數(shù)列;
為等比數(shù)列;
(3)(理)數(shù)列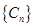 ,滿足
,滿足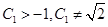 ,
,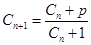 ,其中
,其中 為第(2)小題中確定的正常數(shù),求證:對任意
為第(2)小題中確定的正常數(shù),求證:對任意 ,有
,有 且
且 或
或 且
且 成立.
成立.
(文)設(shè)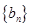 是滿足第(2)小題的等比數(shù)列,求使不等式
是滿足第(2)小題的等比數(shù)列,求使不等式 成立的最小正整數(shù)
成立的最小正整數(shù) .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本題18分)已知橢圓C:![]() 的右焦點為B(1,0),右準(zhǔn)線與x軸的交點為A(5,0),過點A作直線
的右焦點為B(1,0),右準(zhǔn)線與x軸的交點為A(5,0),過點A作直線![]() 交橢圓C于兩個不同的點P、Q.
交橢圓C于兩個不同的點P、Q.
(1)求橢圓C的方程;
(2)求直線![]() 斜率的取值范圍;
斜率的取值范圍;
(3)是否存在直線![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com