
分析 (1)當a=0時,f(x)=-|x|-1,不等式f(2x)+2≥0可化為-|2x|-1+2≥0,解得答案;
(2)當a<0時,$f(x)=a{x^2}-|x|+2a-1=\left\{\begin{array}{l}a{(x-\frac{1}{2a})^2}+3a-1-\frac{1}{4a}(x≥0)\\ a{(x+\frac{1}{2a})^2}+3a-1-\frac{1}{4a}(x<0)\end{array}\right.$結合二次函數的圖象和性質,可得x=0時,f(x)取最大值;
(3)若a>0,分類討論函數圖象的對稱軸與區間[1,2]的位置關系,結合二次函數的圖象和性質,可得g(a)的表達式.
解答 解:(1)當a=0時,f(x)=-|x|-1,
則不等式f(2x)+2≥0可化為-|2x|-1+2≥0,
即|2x|≤1,解之得:x≤0,
則所求不等式的解集為(-∞,0].
(2)當a<0時,$f(x)=a{x^2}-|x|+2a-1=\left\{\begin{array}{l}a{(x-\frac{1}{2a})^2}+3a-1-\frac{1}{4a}(x≥0)\\ a{(x+\frac{1}{2a})^2}+3a-1-\frac{1}{4a}(x<0)\end{array}\right.$,
故當x=0時,f(x)max=f(0)=3a-1(或由奇偶性直接討論x≥0時,函數f(x)的單調性,得到最大值),
(3)當x∈[1,2]時,$f(x)=a{x^2}-x+3a-1=a{(x-\frac{1}{2a})^2}+3a-\frac{1}{4a}-1(a>0)$,
①當$\frac{1}{2a}≤1$時,即$a≥\frac{1}{2}$時,此時x=1時,f(x)min=f(1)=4a-2,
②當$1<\frac{1}{2a}<2$時,即$\frac{1}{4}<a<\frac{1}{2}$時,即$x=\frac{1}{2a}$時,$f{(x)_{min}}=f(\frac{1}{2a})=3a-\frac{1}{4a}-1$,
③當$\frac{1}{2a}≥2$時,即$0<a≤\frac{1}{4}$時,此時x=2時,f(x)min=f(2)=7a-3,
綜上所述可得:$g(a)=\left\{\begin{array}{l}4a-2,a≥\frac{1}{2}\\ 3a-\frac{1}{4a}-1,\frac{1}{4}<a<\frac{1}{2}\\ 7a-3,0<a≤\frac{1}{4}\end{array}\right.$.
點評 本題考查的知識點是二次函數的圖象和性質,熟練掌握二次函數的圖象和性質,是解答的關鍵.


 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
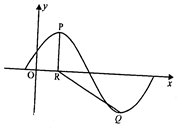 已知函數f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}})$)的部分圖象如圖所示,P,Q分別為該圖象的最高點和最低點,點P的坐標為(2,A),點R的坐標為(2,0).若∠PRQ=$\frac{2π}{3}$,則y=f(x)的最大值是2$\sqrt{3}$.
已知函數f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}})$)的部分圖象如圖所示,P,Q分別為該圖象的最高點和最低點,點P的坐標為(2,A),點R的坐標為(2,0).若∠PRQ=$\frac{2π}{3}$,則y=f(x)的最大值是2$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
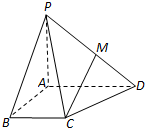 如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面為直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1.
如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面為直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com