
【題目】已知定義在R上的函數(shù)f(x)=|x﹣m|+|x|,m∈N*,存在實(shí)數(shù)x使f(x)<2成立.
(1)求不等式f(x)>8的解;
(2)若α,β≥1,f(α)+f(β)=4,求證:![]() .
.
【答案】(1) {x|x![]() 或x
或x![]() };(2)證明見解析
};(2)證明見解析
【解析】
(1)由絕對值三角不等式可得|x﹣m|+|x|≥|m|,根據(jù)存在實(shí)數(shù)x使f(x)<2成立,求出實(shí)數(shù)m的值,然后解不等式f(x)>8即可.
(2)先由條件求出α+β=3,從而得到![]() ,再利用基本不等式求出最小值即可證明結(jié)論.
,再利用基本不等式求出最小值即可證明結(jié)論.
(1)因?yàn)?/span>|x﹣m|+|x|≥|(x﹣m)﹣x|=|m|,
所以由存在實(shí)數(shù)x使f(x)<2成立,可得|m|<2,
所以﹣2<m<2,因?yàn)?/span>m∈N*,所以m=1,
所以f(x)=|x﹣1|+|x|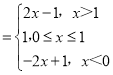 .
.
因?yàn)?/span>f(x)>8,所以![]() 或
或![]() ,
,
所以x![]() 或x
或x![]() ,
,
所以不等式的解集為{x|x![]() 或x
或x![]() };
};
(2)因?yàn)?/span>α,β≥1,所以f(α)+f(β)=2α﹣1+2β﹣1=4,則α+β=3,
所以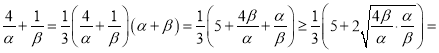 3,
3,
當(dāng)且僅當(dāng)![]() ,即α=2,β=1時取等號,
,即α=2,β=1時取等號,
所以![]() .
.


 導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點(diǎn)![]() 是直角
是直角![]() 斜邊
斜邊![]() 上一動點(diǎn),
上一動點(diǎn),![]()
![]() 將直角
將直角![]() 沿著
沿著![]() 翻折,使
翻折,使![]() 與
與![]() 構(gòu)成直二面角,則翻折后
構(gòu)成直二面角,則翻折后![]() 的最小值是_______.
的最小值是_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:x2+(y-1)2=5,直線l:mx-y+1-m=0(m∈R).
(1)判斷直線l與圓C的位置關(guān)系;
(2)設(shè)直線l與圓C交于A,B兩點(diǎn),若直線l的傾斜角為120°,求弦AB的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】兩縣城![]() 和
和![]() 相距
相距![]() ,現(xiàn)計(jì)劃在兩縣城外位于線段
,現(xiàn)計(jì)劃在兩縣城外位于線段![]() 上選擇一點(diǎn)
上選擇一點(diǎn)![]() 建造一個兩縣城的公共垃圾處理廠,已知垃圾處理廠對城市的影響度與所選地點(diǎn)到城市的的距離關(guān)系最大,其他因素影響較小暫時不考慮,垃圾處理廠對城
建造一個兩縣城的公共垃圾處理廠,已知垃圾處理廠對城市的影響度與所選地點(diǎn)到城市的的距離關(guān)系最大,其他因素影響較小暫時不考慮,垃圾處理廠對城![]() 和城
和城![]() 的總影響度為對城
的總影響度為對城![]() 與城
與城![]() 的影響度之和. 記
的影響度之和. 記![]() 點(diǎn)到城
點(diǎn)到城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理廠對城
處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() ,統(tǒng)計(jì)調(diào)查表明:垃圾處理廠對城
,統(tǒng)計(jì)調(diào)查表明:垃圾處理廠對城![]() 的影響度與所選地點(diǎn)到城
的影響度與所選地點(diǎn)到城![]() 的距離的平方成反比,比例系數(shù)2.7;垃圾處理廠對城
的距離的平方成反比,比例系數(shù)2.7;垃圾處理廠對城![]() 的影響度與所選地點(diǎn)到城
的影響度與所選地點(diǎn)到城![]() 的距離的平方成反比,比例系數(shù)為
的距離的平方成反比,比例系數(shù)為![]() ;且當(dāng)垃圾處理廠
;且當(dāng)垃圾處理廠![]() 與城
與城![]() 距離為
距離為![]() 時對城
時對城![]() 和城
和城![]() 的總影響度為0.029.
的總影響度為0.029.
(1) 將![]() 表示成
表示成![]() 的函數(shù);
的函數(shù);
(2) 討論⑴中函數(shù)的單調(diào)性,并判斷在線段![]() 上是否存在一點(diǎn),使建在此處的垃圾處理廠對城
上是否存在一點(diǎn),使建在此處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點(diǎn)到城
的總影響度最小?若存在,求出該點(diǎn)到城![]() 的距離;若不存在,說明理由.
的距離;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 、
、![]() 是兩個不同的平面,
是兩個不同的平面,![]() 、
、![]() 是兩條不同的直線,有下列命題:
是兩條不同的直線,有下列命題:
①如果![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;
;
②如果![]() ,
,![]() ,那么
,那么![]() ;
;
③如果![]() ,
,![]() ,那么
,那么![]() ;
;
④如果平面![]() 內(nèi)有不共線的三點(diǎn)到平面
內(nèi)有不共線的三點(diǎn)到平面![]() 的距離相等,那么
的距離相等,那么![]() ;
;
其中正確的命題是( )
A.①②B.②③C.②④D.②③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,動圓
,動圓![]() 與圓
與圓![]() 外切,且與直線
外切,且與直線![]() 相切,該動圓圓心
相切,該動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程
的方程
(2)過點(diǎn)![]() 的直線與拋物線相交于
的直線與拋物線相交于![]() 兩點(diǎn),拋物線在點(diǎn)A的切線與
兩點(diǎn),拋物線在點(diǎn)A的切線與![]() 交于點(diǎn)N,求
交于點(diǎn)N,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com