
【題目】給出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的個數是( )
)(x∈(0,1))其中成立的個數是( )
A.0
B.1
C.2
D.3
【答案】B
【解析】解:對于①,x≥ln(x+1)(x>﹣1),構造函數:f(x)=x﹣ln(x+1)(x>﹣1).f′(x)=1﹣ ![]() =
= ![]() ,可得x∈(﹣1,0),函數f(x)遞減,x∈(0,+∞)遞增,故f(x)≥f(0)=0 ∴x≥ln(x+1)(x>﹣1)成立,故
,可得x∈(﹣1,0),函數f(x)遞減,x∈(0,+∞)遞增,故f(x)≥f(0)=0 ∴x≥ln(x+1)(x>﹣1)成立,故 ![]() 成立.
成立.
對于②,取x=1, ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)不成立,故②不成立;
(x>0)不成立,故②不成立;
對于③,ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1)),構造函數g(x)=ln
)(x∈(0,1)),構造函數g(x)=ln ![]() ﹣2(x+
﹣2(x+ ![]() )(x∈(0,1)),
)(x∈(0,1)),
g′(x)= ![]() =
= ![]() 0,∴g(x)在(0,1)遞增,而g(0)=0,故x∈(0,1)時,g(x)>0恒成立,故
0,∴g(x)在(0,1)遞增,而g(0)=0,故x∈(0,1)時,g(x)>0恒成立,故 ![]() 成立.
成立.
故選:B
【考點精析】認真審題,首先需要了解命題的真假判斷與應用(兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系).


科目:高中數學 來源: 題型:
【題目】下表是某廠的產量x與成本y的一組數據:
產量x(千件) | 2 | 3 | 5 | 6 |
成本y(萬元) | 7 | 8 | 9 | 12 |
(Ⅰ)根據表中數據,求出回歸直線的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 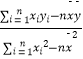 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)預計產量為8千件時的成本.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各式中S的值不可以用算法求解的是( )
A.S=1+2+3+4
B.S=1+2+3+4+…
C.S=1+ ![]() +
+ ![]() +…+
+…+ ![]()
D.S=12+22+32+…+1002
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4—4:坐標系與參數方程】
將圓![]() 上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
(Ⅰ)寫出C的參數方程;
(Ⅱ)設直線![]() 與C的交點為
與C的交點為![]() ,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段
,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段![]() 的中點且與
的中點且與![]() 垂直的直線的極坐標方程.
垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了了解一年內的用水情況,抽取了10天的用水量如表所示:
天數 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/噸 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在這10天中,該公司用水量的平均數是多少?每天用水量的中位數是多少?
(Ⅱ)你認為應該用平均數和中位數中的哪一個數來描述該公司每天的用水量?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com