
【題目】某公司為了了解一年內的用水情況,抽取了10天的用水量如表所示:
天數 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/噸 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在這10天中,該公司用水量的平均數是多少?每天用水量的中位數是多少?
(Ⅱ)你認為應該用平均數和中位數中的哪一個數來描述該公司每天的用水量?
科目:高中數學 來源: 題型:
【題目】給出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的個數是( )
)(x∈(0,1))其中成立的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() 的圖象過點(0,﹣1).
的圖象過點(0,﹣1).
(1)求實數a的值;
(2)若f(x)=m+ ![]() (m,n是常數),求實數m,n的值;
(m,n是常數),求實數m,n的值;
(3)用定義法證明:函數f(x)在(3,+∞)上是單調減函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (a是常數,且a>0).對于下列命題:①函數f(x)的最小值是﹣1;②函數f(x)在R上是單調函數;③若f(x)>0在[
(a是常數,且a>0).對于下列命題:①函數f(x)的最小值是﹣1;②函數f(x)在R上是單調函數;③若f(x)>0在[ ![]() ,+∞)上恒成立,則a的取值范圍是a>1;④對任意x1<0,x2<0且x1≠x2 , 恒有f(
,+∞)上恒成立,則a的取值范圍是a>1;④對任意x1<0,x2<0且x1≠x2 , 恒有f( ![]() )>
)> ![]() .其中正確命題的序號是( )
.其中正確命題的序號是( )
A.①②
B.①③
C.③④
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺機器按不同的轉速生產出來的某機械零件有一些會有缺點,每小時生產有缺點零件的多少,隨機器的運轉的速度而變化,具有線性相關關系,下表為抽樣試驗的結果:
轉速x(轉/秒) | 8 | 10 | 12 | 14 | 16 |
每小時生產有缺點的零件數y(件) | 5 | 7 | 8 | 9 | 11 |
參考公式: ![]() ,
, ![]() =
= 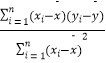 =
= 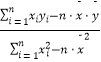 .
.
(1)如果y對x有線性相關關系,求回歸方程;
(2)若實際生產中,允許每小時生產的產品中有缺點的零件最多有10個,那么機器的運轉速度應控制在設么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)是定義在R上的可導函數,且滿足(x﹣1)f′(x)≥0,則必有( )
A.f(0)+f(2)<2f(1)
B.f(0)+f(2)>2f(1)
C.f(0)+f(2)≤2f(1)
D.f(0)+f(2)≥2f(1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且Sn=2n2+n,n∈N* , 數列{bn}滿足an=4log2bn+3,n∈N* .
(1)求an , bn;
(2)求數列{anbn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知[x)表示大于x的最小整數,例如[3)=4,[﹣1,3)=﹣1,下列命題中正確的是( ) ①函數f(x)=[x)﹣x的值域是(0,1]
②若{an}是等差數列,則{[an)}也是等差數列
③若{an}是等比數列,則{[an)}也是等比數列
④若x∈(1,2017),則方程[x)﹣x=sin ![]() x有1007個根.
x有1007個根.
A.②
B.③④
C.①
D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin( ![]() ﹣x)sinx﹣
﹣x)sinx﹣ ![]() cos2x. (I)求f(x)的最小正周期和最大值;
cos2x. (I)求f(x)的最小正周期和最大值;
(II)討論f(x)在[ ![]() ,
, ![]() ]上的單調性.
]上的單調性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com