
【題目】函數g(x)=ax3+2(1﹣a)x2﹣3ax在區間(﹣∞, ![]() )內單調遞減,則a的取值范圍是 .
)內單調遞減,則a的取值范圍是 .
【答案】﹣1≤a≤0
【解析】解:∵g′(x)=3ax2+4(1﹣a)x﹣3a,g(x)在(﹣∞,a/3)遞減, 則g′(x)在(﹣∞,a/3)上小于等于0
①a=0時,g′(x)≤0,解得:x≤0,即g(x)的減區間是(﹣∞,0),
∴ ![]() ≤0,才能g(x)在(﹣∞,
≤0,才能g(x)在(﹣∞, ![]() )遞減,解得a=0
)遞減,解得a=0
②a>0,g′(x)是一個開口向上的拋物線,
要使g′(x)在(﹣∞, ![]() )上小于等于0 解得:a無解
)上小于等于0 解得:a無解
③a<0,g′(x)是一個開口向下的拋物線,
設g′(x)與x軸的左右兩交點為A(x1 , 0),B(x2 , 0)
由韋達定理,知x1+x2=﹣ ![]() ,x1x2=﹣1,
,x1x2=﹣1,
解得:x1=﹣ ![]() ,
,
則在A左邊和B右邊的部分g′(x)≤0 又知g(x)在(﹣∞, ![]() )遞減,
)遞減,
即g′(x)在(﹣∞, ![]() )上小于等于0,
)上小于等于0,
∴x1≥ ![]() ,解得﹣1≤a≤5,取交集,得﹣1≤a<0,
,解得﹣1≤a≤5,取交集,得﹣1≤a<0,
∴a的取值范圍是﹣1≤a≤0.
【考點精析】通過靈活運用利用導數研究函數的單調性,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減即可以解答此題.
在這個區間單調遞減即可以解答此題.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】在對某漁業產品的質量調研中,從甲、乙兩地出產的該產品中各隨機抽取10件,測量該產品中某種元素的含量(單位:毫克).如圖是測量數據的莖葉圖: 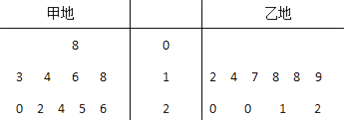
規定:當產品中的此種元素含量≥15毫克時為優質品.
(Ⅰ)試用上述樣本數據估計甲、乙兩地該產品的優質品率(優質品件數/總件數);
(Ⅱ)從乙地抽出的上述10件產品中,隨機抽取3件,求抽到的3件產品中優質品數ξ的分布列及數學期望E(ξ).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在△ABC中,D、F分別是BC、AC的中點, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;
;
(2)求證:B、E、F三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若關于x的方程f(f(x))=0有且只有一個實數解,則實數a的取值范圍是( )
,若關于x的方程f(f(x))=0有且只有一個實數解,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(﹣∞,0]∪(0,1)
C.(﹣∞,0)∪(0,1]
D.(﹣∞,0)∪(0,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)在(﹣∞,0)∪(0,+∞)上有定義,在(0,+∞)上是增函數,f(1)=0,又知函數g(θ)=sin2θ+mcosθ﹣2m, ![]() ,集合M={m|恒有g(θ)<0},N={m|恒有f(g(θ))<0},求M∩N.
,集合M={m|恒有g(θ)<0},N={m|恒有f(g(θ))<0},求M∩N.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的個數是( )
)(x∈(0,1))其中成立的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (a是常數,且a>0).對于下列命題:①函數f(x)的最小值是﹣1;②函數f(x)在R上是單調函數;③若f(x)>0在[
(a是常數,且a>0).對于下列命題:①函數f(x)的最小值是﹣1;②函數f(x)在R上是單調函數;③若f(x)>0在[ ![]() ,+∞)上恒成立,則a的取值范圍是a>1;④對任意x1<0,x2<0且x1≠x2 , 恒有f(
,+∞)上恒成立,則a的取值范圍是a>1;④對任意x1<0,x2<0且x1≠x2 , 恒有f( ![]() )>
)> ![]() .其中正確命題的序號是( )
.其中正確命題的序號是( )
A.①②
B.①③
C.③④
D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com