

| A. | 0 | B. | 0或-1 | C. | ±1 | D. | 1 |
分析 分析如圖所示的程序語言知該程序運(yùn)行后輸出分段函數(shù),
討論x的取值,求出y=1時(shí)x的值即可.
解答 解:根據(jù)如圖所示的程序語言知,該程序運(yùn)行后輸出函數(shù)
y=$\left\{\begin{array}{l}{{2}^{x},x≥0}\\{|x|,x<0}\end{array}\right.$;
當(dāng)x≥0時(shí),y=2x=1,解得x=0;
當(dāng)x<0時(shí),y=|x|=1,解得x=-1;
綜上,輸出y的值為1時(shí),輸入x的值為0或-1.
故選:B.
點(diǎn)評(píng) 本題考查了條件語句和分段函數(shù)的問題,是基礎(chǔ)題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題

| A. | 2π | B. | $\frac{3π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{7π}{6}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | p∧(?q) | B. | (?p)∧q | C. | (?p)∧(?q) | D. | p∧q |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
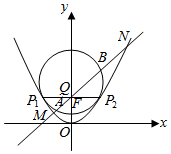 如圖,拋物線C:x2=2py(p>0)的準(zhǔn)線為y=-1,取過焦點(diǎn)F且平行于x軸的直線與拋物線交于不同的兩點(diǎn)P1,P2,過P1,P2作圓心為Q的圓,使拋物線上其余點(diǎn)均在圓外,且∠P1QP2=90°.
如圖,拋物線C:x2=2py(p>0)的準(zhǔn)線為y=-1,取過焦點(diǎn)F且平行于x軸的直線與拋物線交于不同的兩點(diǎn)P1,P2,過P1,P2作圓心為Q的圓,使拋物線上其余點(diǎn)均在圓外,且∠P1QP2=90°.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{1}{5}$ | B. | -$\frac{1}{5}$i | C. | $\frac{1}{5}$ | D. | $\frac{1}{5}$i |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com