
【題目】設(shè)函數(shù)![]() .
.
(1)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 使得不等式
使得不等式![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
(2) ![]() ;
;
【解析】
(1)求函數(shù)的導(dǎo)數(shù),研究函數(shù)的單調(diào)性即可
(2)利用參數(shù)分離法轉(zhuǎn)化為最值問題,構(gòu)造函數(shù)求函數(shù)的最值即可
(1)當![]() 時,
時,![]() ,
,![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
故函數(shù)![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(2)![]() ,使得不等式
,使得不等式![]() 成立.
成立.
即![]() ,使得不等式
,使得不等式![]() 成立.
成立.
等價于![]() ,使得不等式
,使得不等式![]() 成立.
成立.
令![]() ,
,![]() ,則
,則![]() .
.
設(shè)![]() ,則
,則![]() ,
,
顯然函數(shù)![]() 在
在![]() 是增函數(shù).
是增函數(shù).
因為![]() ,
,![]() ,且函數(shù)
,且函數(shù)![]() 的圖象在
的圖象在![]() 上連續(xù),
上連續(xù),
所以![]() ,使得
,使得![]() ,
,
且當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以函數(shù)![]() 存在極小值
存在極小值![]() ,也是最小值.
,也是最小值.
所以![]() ,
,
其中![]() ,滿足
,滿足![]() ,即
,即![]() .
.
所以![]() ,即
,即![]() .
.
所以![]()
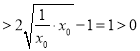 .
.
所以當![]() 時,
時,![]() .
.
所以![]() 在
在![]() 內(nèi)單調(diào)遞增.
內(nèi)單調(diào)遞增.
所以![]()
![]() .
.
所以有![]() ,
,
即實數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.


 奪冠訓(xùn)練單元期末沖刺100分系列答案
奪冠訓(xùn)練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】
已知函數(shù)f(x)=![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲線y=f(x)在點(2,f(2))處的切線方程;
(Ⅱ)若在區(qū)間![]() 上,f(x)>0恒成立,求a的取值范圍.
上,f(x)>0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)實數(shù)![]() ,橢圓
,橢圓![]() 的右焦點為F,過F且斜率為k的直線交D于P、Q兩點,若線段PQ的中點為N,點O是坐標原點,直線ON交直線
的右焦點為F,過F且斜率為k的直線交D于P、Q兩點,若線段PQ的中點為N,點O是坐標原點,直線ON交直線![]() 于點M.
于點M.
![]() 若點P的橫坐標為1,求點Q的橫坐標;
若點P的橫坐標為1,求點Q的橫坐標;
![]() 求證:
求證:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2sinx﹣xcosx﹣x,f'(x)為f(x)的導(dǎo)數(shù).
(1)求曲線![]() 在點A(0,f(0))處的切線方程;
在點A(0,f(0))處的切線方程;
(2)設(shè)![]() ,求
,求![]() 在區(qū)間[0,π]上的最大值和最小值。
在區(qū)間[0,π]上的最大值和最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的兩個焦點,
的兩個焦點,![]() 為坐標原點,離心率為
為坐標原點,離心率為![]() ,點
,點![]() 在橢圓上.
在橢圓上.
(1)求橢圓的標準方程;
(2)![]() 為橢圓上三個動點,
為橢圓上三個動點,![]() 在第二象限,
在第二象限,![]() 關(guān)于原點對稱,且
關(guān)于原點對稱,且![]() ,判斷
,判斷![]() 是否存在最小值,若存在,求出該最小值,并求出此時點
是否存在最小值,若存在,求出該最小值,并求出此時點![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,已知G與E分別為
,已知G與E分別為![]() 和
和![]() 的中點,D和F分別為線段AC和AB上的動點(不包括端點),若
的中點,D和F分別為線段AC和AB上的動點(不包括端點),若![]() ,則線段DF的長度的平方取值范圍為( ).
,則線段DF的長度的平方取值范圍為( ).

A.![]() B.
B.![]() C.
C. D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于數(shù)列![]() ,給出下列命題:①數(shù)列
,給出下列命題:①數(shù)列![]() 滿足
滿足![]() ,則數(shù)列
,則數(shù)列![]() 為公比為2的等比數(shù)列;②“
為公比為2的等比數(shù)列;②“![]() ,
,![]() 的等比中項為
的等比中項為![]() ”是“
”是“![]() ”的充分不必要條件:③數(shù)列
”的充分不必要條件:③數(shù)列![]() 是公比為
是公比為![]() 的等比數(shù)列,則其前
的等比數(shù)列,則其前![]() 項和
項和![]() ;④等比數(shù)列
;④等比數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() ,
,![]() ,
,![]() 成等比數(shù)列,其中假命題的序號是( )
成等比數(shù)列,其中假命題的序號是( )
A.②B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知遞增的等差數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比數(shù)列,且
成等比數(shù)列,且![]() .
.
(1)求數(shù)列![]() 的通項公式及前
的通項公式及前![]() 項和
項和![]() ;
;
(2)設(shè)![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 為常數(shù).
為常數(shù).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 有兩個不同的零點
有兩個不同的零點![]() ,
,![]() ,
,
①當![]() 時,求
時,求![]() 的最小值;
的最小值;
②當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com