
分析 (1)利用f(x)在x=1時取極值,則求出f′(x)得到f′(1)=0,解出求出a即可.
(2)利用函數的導數,判斷函數的單調性求解函數的極值即可.
解答 解:(1)∵f′(x)=3x2+6ax-9,f(x)在x=1時取得極值,
∴f′(1)=3+6a-9=0
∴a=1.
(2)由(1)可得f′(x)=3x2+6x-9=3(x-1)(x+3).
函數的極值點為x=1,x=-3,
當x<-3,或x>1時,函數是增函數,x∈(-3,1)時,函數是減函數,
x=-3函數取得極大值,極大值為:f(-3)=32,
x=1時,函數取得極小值,極小值為:f(1)=0.
點評 本題考查學生利用導數研究函數極值的能力,考查學生的計算能力,是中檔題.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 年齡(單位:歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
| 贊成人數 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
| 贊成 | |||
| 不贊成 | |||
| 合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
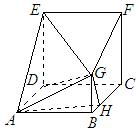 在多面體ABCDEFG中,四邊形ABCD與CDEF是邊長均為a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一點,且AB=2BG=4BH
在多面體ABCDEFG中,四邊形ABCD與CDEF是邊長均為a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一點,且AB=2BG=4BH 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 2008 | C. | 2017 | D. | 4017 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com