
分析 (1)根據(jù)向量的數(shù)量積公式和向量的夾角公式得到關(guān)于x,y的方程組,解得即可,
(2)先根據(jù)向量的垂直求出向量$\overrightarrow{n}$,再根據(jù)向量的坐標(biāo)的運(yùn)算和三角函數(shù)的化簡(jiǎn),即可求出$|\overrightarrow p+\overrightarrow n|$.
解答 解:(1)設(shè)$\overrightarrow{n}$=(x,y),
∵向量$\overrightarrow m=(1,1)$,向量$\overrightarrow{m}$與向量$\overrightarrow{n}$的夾角為135°,且$\overrightarrow{m}$•$\overrightarrow{n}$=-1.
∴$\frac{-1}{\sqrt{{x}^{2}+{y}^{2}}•\sqrt{2}}=cos135°$,即x2+y2=1,且x+y=-1,
解得x=-1,y=0,或x=0,y=-1
∴$\overrightarrow n=(-1,0)或(0,-1)$,
(2)∵$\overrightarrow n$與$\overrightarrow q=(1,0)$的夾角為$\frac{π}{2}$,
∴$\overrightarrow{n}$•$\overrightarrow{q}$=x=0,
∴$\overrightarrow{n}$=(0,-1),
∴$\overrightarrow{p}$+$\overrightarrow{n}$=$(cosA,2{cos^2}\frac{C}{2}-1)=(cosA,cosA)$,
∴$|\overrightarrow p+\overrightarrow n|=1$
點(diǎn)評(píng) 本題考查了向量的數(shù)量積公式和向量的垂直以及三角函數(shù)的化簡(jiǎn),屬于中檔題.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
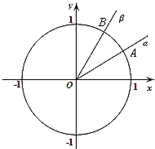 如圖,在平面直角坐標(biāo)系中,銳角α,β的終邊分別與單位圓交于A,B兩點(diǎn).
如圖,在平面直角坐標(biāo)系中,銳角α,β的終邊分別與單位圓交于A,B兩點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
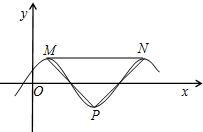 函數(shù)f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)(ω>0)的部分圖象如圖所示,設(shè)M,N是圖象上的最高點(diǎn),P是圖象上的最低點(diǎn),若△PMN為等腰直角三角形,則ω=( )
函數(shù)f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)(ω>0)的部分圖象如圖所示,設(shè)M,N是圖象上的最高點(diǎn),P是圖象上的最低點(diǎn),若△PMN為等腰直角三角形,則ω=( )| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com