
【題目】△ABC中,A(0,1),AB邊上的高CD所在直線的方程為x+2y-4=0,AC邊上的中線BE所在直線的方程為2x+y-3=0.
(1)求直線AB的方程;
(2)求直線BC的方程;
(3)求△BDE的面積.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】試題分析:(1)由![]() 所在直線的方程求出直線
所在直線的方程求出直線![]() 的斜率,再由點斜式寫出
的斜率,再由點斜式寫出![]() 的直線方程;
的直線方程;
(2)先求出點![]() ,點
,點![]() 的坐標,再寫出
的坐標,再寫出![]() 的直線方程;
的直線方程;
(3)由點到直線的距離求出![]() 到
到![]() 的距離
的距離![]() ,以及
,以及![]() 到
到![]() 的距離
的距離![]() ,計算
,計算![]() 即可或求出
即可或求出![]() 到
到![]() 的距離
的距離![]() ,計算
,計算![]() .
.
試題解析:
(1)由已知得直線AB的斜率為2,
∴AB邊所在的直線方程為y-1=2(x-0),
即2x-y+1=0.
(2)由![]() ,得
,得![]() .
.
即直線AB與直線BE的交點為B(![]() ,2).
,2).
設C(m,n),
則由已知條件得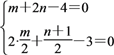 ,
,
解得![]() ,∴C(2,1).
,∴C(2,1).
∴BC邊所在直線的方程為![]() =
=![]() ,即2x+3y-7=0.
,即2x+3y-7=0.
(3)∵E是線段AC的中點,∴E(1,1).
∴|BE|=![]() =
=![]() ,
,
由![]() ,得
,得![]() .
.
∴D(![]() ,
,![]() ),
),
∴D到BE的距離為d=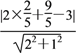 =
=![]() ,
,
∴S△BDE=![]() ·d·|BE|=
·d·|BE|=![]() .
.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】已知某產品出廠前需要依次通過三道嚴格的審核程序,三道審核程序通過的概率依次為 ![]() ,
, ![]() ,
, ![]() ,每道程序是相互獨立的,且一旦審核不通過就停止審核,該產品只有三道程序都通過才能出廠銷售 (Ⅰ)求審核過程中只通過兩道程序的概率;
,每道程序是相互獨立的,且一旦審核不通過就停止審核,該產品只有三道程序都通過才能出廠銷售 (Ⅰ)求審核過程中只通過兩道程序的概率;
(Ⅱ)現有3件該產品進入審核,記這3件產品可以出廠銷售的件數為X,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:實數x滿足x2﹣4ax+3a2<0,其中a>0;命題q:實數x滿足|x﹣3|≤1.
(1)若a=1,且p∧q為真,求實數x的取值范圍;
(2)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的奇函數y=f(x)的導函數為y=f′(x),當x≠0時, ![]() >0,若a=f(1),b=﹣2f(﹣2),c=(ln
>0,若a=f(1),b=﹣2f(﹣2),c=(ln ![]() )f(ln
)f(ln ![]() ),則a,b,c的大小關系正確的是( )
),則a,b,c的大小關系正確的是( )
A.a<c<b
B.b<c<a
C.a<b<c
D.c<a<b
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次測量中得到的A樣本數據如下:82,84,84,86,86,86,88,88,88,88,若樣本B數據恰好是樣本A數據都加上2后所得數據,則A,B兩樣本的下列數字特征對應相同的是( )
A. 眾數 B. 平均數
C. 中位數 D. 標準差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦點分別為F1、F2 , 點P(x0 ,
=1(a>0,b>0)的左、右焦點分別為F1、F2 , 點P(x0 , ![]() )為雙曲線上一點,若△PF1F2的內切圓半徑為1,且圓心G到原點O的距離為
)為雙曲線上一點,若△PF1F2的內切圓半徑為1,且圓心G到原點O的距離為 ![]() ,則雙曲線的離心率是 .
,則雙曲線的離心率是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下四個說法: ①繪制頻率分布直方圖時,各小長方形的面積等于相應各組的組距;
②在刻畫回歸模型的擬合效果時,相關指數R2的值越大,說明擬合的效果越好;
③設隨機變量ξ服從正態分布N(4,22),則p(ξ>4)= ![]()
④對分類變量X與Y,若它們的隨機變量K2的觀測值k越小,則判斷“X與Y有關系”的把握程度越大.
其中正確的說法是( )
A.①④
B.②③
C.①③
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法: ①將一組數據中的每個數據都加上或減去同一個常數后,均值與方差都不變;
②設有一個回歸方程 ![]() ,變量x增加一個單位時,y平均增加3個單位;
,變量x增加一個單位時,y平均增加3個單位;
③線性回歸方程 ![]() 必經過點
必經過點 ![]() ;
;
④在吸煙與患肺病這兩個分類變量的計算中,從獨立性檢驗知,有99%的把握認為吸煙與患肺病有關系時,我們說現有100人吸煙,那么其中有99人患肺病.其中錯誤的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com