
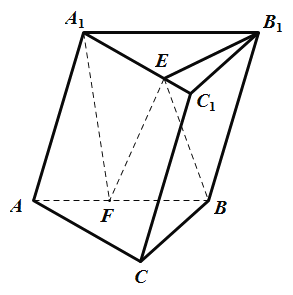
【題目】三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,AB=AA1=A1B=4,BC=2,AC=2![]() ,點F為AB的中點,點E為線段A1C1上的動點.
,點F為AB的中點,點E為線段A1C1上的動點.
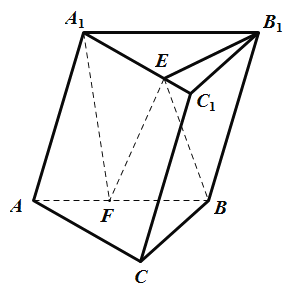
(1)求證:BC⊥平面A1EF;
(2)若∠B1EC1=60°,求四面體A1B1EF的體積.
【答案】(1)證明見解析.(2)![]()
【解析】
(1)利用等邊三角形的性質可得:A1F⊥AB.利用線面、面面垂直的判定定理與性質定理可得:A1F⊥BC.利用勾股定理的逆定理可得:BC⊥AC.進而證明結論.
(2)利用直角三角形的邊角關系可得:EC1![]() ,A1E.由(I)可得:A1F⊥底面A1B1C1,A1F⊥A1E,A1F=2
,A1E.由(I)可得:A1F⊥底面A1B1C1,A1F⊥A1E,A1F=2![]() .可得△A1EF的面積S.由(I)可得:BC⊥平面A1EF,可得B1C1⊥平面A1EF,即可得出四面體A1B1EF的體積.
.可得△A1EF的面積S.由(I)可得:BC⊥平面A1EF,可得B1C1⊥平面A1EF,即可得出四面體A1B1EF的體積.
(1)∵AB=AA1=A1B,點F為AB的中點,∴A1F⊥AB,
∵平面AA1B1B⊥平面ABC,平面AA1B1B∩平面ABC=AB,
∴A1F⊥平面ABC,BC平面ABC,∴A1F⊥BC.
∵AB=4,BC=2,AC=2![]() ,∴AB2=BC2+AC2,∴∠ACB=90°,∴BC⊥AC.
,∴AB2=BC2+AC2,∴∠ACB=90°,∴BC⊥AC.
∵AC∥A1C1,∴BC⊥A1C1,又A1F∩A1E=A1,∴BC⊥平面A1EF;
(2)∵∠B1EC1=60°,∴EC1![]() ,∴A1E=2
,∴A1E=2![]() .
.
由(1)可得:A1F⊥底面A1B1C1,∴A1F⊥A1E,A1F=2![]() .
.
∴△A1EF的面積S![]() 4.
4.
由(1)可得:BC⊥平面A1EF,∵B1C1∥BC,∴B1C1⊥平面A1EF,
∴四面體A1B1EF的體積![]() SB1C1
SB1C1![]() 4×2
4×2![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線C1:x2=2py(p>0),圓C2:x2+y2﹣8y+12=0的圓心M到拋物線C1的準線的距離為![]() ,點P是拋物線C1上一點,過點P,M的直線交拋物線C1于另一點Q,且|PM|=2|MQ|,過點P作圓C2的兩條切線,切點為A、B.
,點P是拋物線C1上一點,過點P,M的直線交拋物線C1于另一點Q,且|PM|=2|MQ|,過點P作圓C2的兩條切線,切點為A、B.
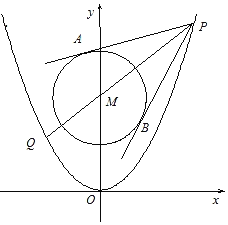
(Ⅰ)求拋物線C1的方程;
(Ⅱ)求直線PQ的方程及![]()
![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】紙張的規格是指紙張制成后,經過修整切邊,裁成一定的尺寸.現在我國采用國際標準,規定以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 等標記來表示紙張的幅面規格.復印紙幅面規格只采用
等標記來表示紙張的幅面規格.復印紙幅面規格只采用![]() 系列和
系列和![]() 系列,其中系列的幅面規格為:①
系列,其中系列的幅面規格為:①![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所有規格的紙張的幅寬(以
所有規格的紙張的幅寬(以![]() 表示)和長度(以
表示)和長度(以![]() 表示)的比例關系都為
表示)的比例關系都為![]() ;②將
;②將![]() 紙張沿長度方向對開成兩等分,便成為
紙張沿長度方向對開成兩等分,便成為![]() 規格,
規格,![]() 紙張沿長度方向對開成兩等分,便成為
紙張沿長度方向對開成兩等分,便成為![]() 規格,…,如此對開至
規格,…,如此對開至![]() 規格.現有
規格.現有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 紙各一張.若
紙各一張.若![]() 紙的寬度為
紙的寬度為![]() ,則
,則![]() 紙的面積為________
紙的面積為________![]() ;這
;這![]() 張紙的面積之和等于________
張紙的面積之和等于________![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
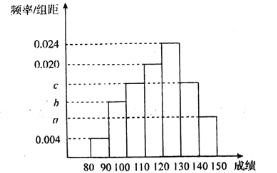
【題目】高三年級某班50名學生期中考試數學成績的頻率分布直方圖如圖所示,成績分組區間為:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差數列且
.其中a,b,c成等差數列且![]() .物理成績統計如表.(說明:數學滿分150分,物理滿分100分)
.物理成績統計如表.(說明:數學滿分150分,物理滿分100分)
分組 |
|
|
|
|
|
頻數 | 6 | 9 | 20 | 10 | 5 |
(1)根據頻率分布直方圖,請估計數學成績的平均分;
(2)根據物理成績統計表,請估計物理成績的中位數;
(3)若數學成績不低于140分的為“優”,物理成績不低于90分的為“優”,已知本班中至少有一個“優”同學總數為6人,從此6人中隨機抽取3人,記X為抽到兩個“優”的學生人數,求X的分布列和期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】手機運動計步已成為一種時尚,某中學統計了該校教職工一天行走步數(單位:百步),繪制出如下頻率分布直方圖:
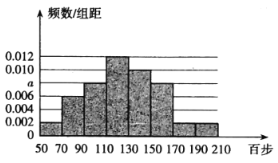
(Ⅰ)求直方圖中![]() 的值,并由頻率分布直方圖估計該校教職工一天步行數的中位數;
的值,并由頻率分布直方圖估計該校教職工一天步行數的中位數;
(Ⅱ)若該校有教職工175人,試估計一天行走步數不大于130百步的人數;
(Ⅲ)在(Ⅱ)的條件下該校從行走步數大于150百步的3組教職工中用分層抽樣的方法選取6人參加遠足活動,再從6人中選取2人擔任領隊,求這兩人均來自區間![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是橢圓
是橢圓![]() 的左右焦點,橢圓與
的左右焦點,橢圓與![]() 軸正半軸交于點
軸正半軸交于點![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,且
,且![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)![]() 為橢圓
為橢圓![]() 上任意一點,過
上任意一點,過![]() ,
,![]() 分別作直線
分別作直線![]() ,
,![]() ,且
,且![]() 與
與![]() 相交于
相交于![]() 軸上方一點
軸上方一點![]() ,當
,當![]() 時,求
時,求![]() ,
,![]() 兩點間距離的最大值.
兩點間距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx-a![]() .
.
(1)若a=-1,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若f(x)![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,菱形ABCD與正三角形BCE的邊長均為2,它們所在的平面互相垂直,DF⊥平面ABCD且DF![]() .
.
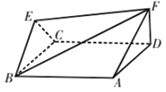
(1)求證:EF//平面ABCD;
(2)若∠ABC=∠BCE,求二面角A﹣BF﹣E的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最大值為
的最大值為![]() ,其圖象相鄰兩條對稱軸之間的距離為
,其圖象相鄰兩條對稱軸之間的距離為![]() ,且
,且![]() 的圖象關于點
的圖象關于點![]() 對稱,則下列判斷正確的是( )
對稱,則下列判斷正確的是( )
A.要得到函數![]() 的圖象,只需將
的圖象,只需將![]() 向右平移
向右平移![]() 個單位
個單位
B.函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱
對稱
C.當![]() 時,函數
時,函數![]() 的最小值為
的最小值為![]()
D.函數![]() 在
在![]() 上單調遞增
上單調遞增
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com