
【題目】已知函數![]() ,
,
(1)求![]() 的最大值;
的最大值;
(2)若對于任意的![]() ,不等式
,不等式![]() 恒成立,求整數a的最小值.(參考數據
恒成立,求整數a的最小值.(參考數據![]() ,
,![]() )
)
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,左、右頂點分別為
,左、右頂點分別為![]() ,
,![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 為等邊三角形,過點
為等邊三角形,過點![]() 的直線與橢圓
的直線與橢圓![]() 在
在![]() 軸右側的部分交于
軸右側的部分交于![]() 、
、![]() 兩點,
兩點,![]() 為坐標原點.
為坐標原點.

(1)求橢圓的標準方程;
(2)求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以坐標原點為極點,以![]() 軸的非負半軸為極軸建立極坐標系,已知曲線
軸的非負半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)點![]() 在曲線
在曲線![]() 上,且曲線
上,且曲線![]() 在點
在點![]() 處的切線與直線:
處的切線與直線:![]() 垂直,求點
垂直,求點![]() 的直角坐標;
的直角坐標;
(2)設直線![]() 與曲線
與曲線![]() 有且只有一個公共點,求直線
有且只有一個公共點,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
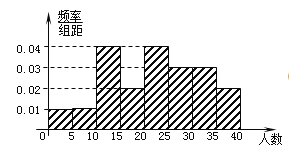
【題目】某普通高中為了解本校高三年級學生數學學習情況,對一模考試數學成績進行分析,從中抽取了![]() 名學生的成績作為樣本進行統計(該校全體學生的成績均在
名學生的成績作為樣本進行統計(該校全體學生的成績均在![]() ),按下列分組
),按下列分組![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 作出頻率分布直方圖,如圖
作出頻率分布直方圖,如圖![]() ;樣本中分數在
;樣本中分數在![]() 內的所有數據的莖葉圖如圖
內的所有數據的莖葉圖如圖![]() :
:

根據往年錄取數據劃出預錄分數線,分數區間與可能被錄取院校層次如表.

(1)求![]() 的值及頻率分布直方圖中的
的值及頻率分布直方圖中的![]() 值;
值;
(2)根據樣本估計總體的思想,以事件發生的頻率作為概率,若在該校高三年級學生中任取![]() 人,求此
人,求此![]() 人都不能錄取為專科的概率;
人都不能錄取為專科的概率;
(3)在選取的樣本中,從可能錄取為自招和專科兩個層次的學生中隨機抽取![]() 名學生進行調研,用
名學生進行調研,用![]() 表示所抽取的
表示所抽取的![]() 名學生中為自招的人數,求隨機變量
名學生中為自招的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與短軸的兩端點組成一個正三角形的三個頂點,且橢圓經過點
的一個焦點與短軸的兩端點組成一個正三角形的三個頂點,且橢圓經過點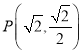 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以線段
兩點,且以線段![]() 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天文學中為了衡量星星的明暗程度,古希臘天文學家喜帕恰斯(![]() ,又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小,星星就越亮;星等的數值越大,它的光就越暗.到了1850年,由于光度計在天體光度測量中的應用,英國天文學家普森(
,又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小,星星就越亮;星等的數值越大,它的光就越暗.到了1850年,由于光度計在天體光度測量中的應用,英國天文學家普森(![]() )又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足
)又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足![]() .其中星等為
.其中星等為![]() 的星的亮度為
的星的亮度為![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,則與
倍,則與![]() 最接近的是(當
最接近的是(當![]() 較小時,
較小時, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某教研機構隨機抽取某校20個班級,調查各班關注漢字聽寫大賽的學生人數,根據所得數據的莖葉圖,以組距為5將數據分組成![]() 時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( )
時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( )
A. 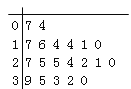 B.
B. 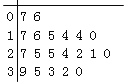
C. 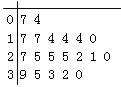 D.
D. 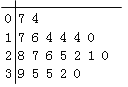
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 的焦點,點
的焦點,點![]() 在
在![]() 軸上,
軸上,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,經過點
,經過點![]() 且垂直于
且垂直于![]() 軸的直線與拋物線
軸的直線與拋物線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 到直線
到直線![]() 的最大距離.
的最大距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com