
【題目】在1與2之間插入![]() 個正數
個正數![]() ,使這
,使這![]() 個數成等比數列;又在1與2之間插入
個數成等比數列;又在1與2之間插入![]() 個正數
個正數![]() ,使這
,使這![]() 個數成等差數列.記
個數成等差數列.記![]() .
.
(1)求數列![]() 和
和![]() 的通項;
的通項;
(2)當![]() 時,比較
時,比較![]() 與
與![]() 大小并證明結論.
大小并證明結論.
【答案】(1)![]() ;(2)
;(2)![]() ;證明見解析;
;證明見解析;
【解析】
(1)由1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等比數列,結合等比數列的性質可得,
成等比數列,結合等比數列的性質可得,![]() ,從而可求
,從而可求![]() ;1,
;1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,2這
,2這![]() 個數成等差數列.利用等差數列的性質可得
個數成等差數列.利用等差數列的性質可得![]() 從而可求
從而可求![]() .
.
(2)由(1)可求![]() ,
,![]() ,轉化比較
,轉化比較![]() ,
,![]() 的大小,先取
的大小,先取![]() ,8,9代入計算,觀察
,8,9代入計算,觀察![]() 與
與![]() 的大小,做出猜想,利用數學歸納法進行證明.
的大小,做出猜想,利用數學歸納法進行證明.
(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,2成等比數列,
,2成等比數列,
![]() ,
,
![]() ,
,
![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,2成等差數列,
,2成等差數列,
![]() ,
,
![]()
![]() .
.
所以,數列![]() 的通項
的通項![]() ,數列
,數列![]() 的通項
的通項![]() .
.
(2)![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
要比較![]() 和
和![]() 的大小,只需比較
的大小,只需比較![]() 與
與![]() 的大小,
的大小,
也即比較當![]() 時,
時,![]() 與
與![]() 的大小.
的大小.
當![]() 時,
時,![]() ,
,![]() ,得知
,得知![]() ,
,
經驗證![]() ,
,![]() 時,均有命題
時,均有命題![]() 成立.
成立.
猜想當![]() 時有
時有![]() .用數學歸納法證明.
.用數學歸納法證明.
①當![]() 時,已驗證
時,已驗證![]() ,命題成立.
,命題成立.
②假設![]() 時,命題成立,即
時,命題成立,即![]() ,
,
那么![]() ,
,
又當![]() 時,有
時,有![]() ,
,
![]()
![]() .
.
這就是說,當![]() 時,命題
時,命題![]() 成立.
成立.
根據①、②,可知命題對于![]() 都成立.
都成立.
故當![]() 時,
時,![]() .
.


科目:高中數學 來源: 題型:
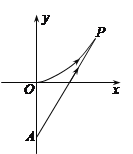
【題目】海事救援船對一艘失事船進行定位:以失事船的當前位置為原點,以正北方向為y軸正方向建立平面直角坐標系(以1海里為單位長度),則救援船恰在失事船的正南方向12海
里A處,如圖. 現假設:①失事船的移動路徑可視為拋物線![]() ;②定位后救援船即刻沿直線勻速前往救援;③救援船出發
;②定位后救援船即刻沿直線勻速前往救援;③救援船出發![]() 小時后,失事船所在位置的橫坐標為
小時后,失事船所在位置的橫坐標為![]() .
.
(1)當![]() 時,寫出失事船所在位置P的縱坐標. 若此時兩船恰好會合,求救援船速度的大小和方向;
時,寫出失事船所在位置P的縱坐標. 若此時兩船恰好會合,求救援船速度的大小和方向;
(2)問救援船的時速至少是多少海里才能追上失事船?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知常數![]() ,向量
,向量![]() ,
,![]() ,經過定點
,經過定點![]() 且以
且以![]() 為方向向量的直線與經過定點
為方向向量的直線與經過定點![]() 且以
且以![]() 為方向向量的直線交于點
為方向向量的直線交于點![]() ,其中
,其中![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若![]() ,過
,過![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取一個年份,對西安市該年4月份的天氣情況進行統計,結果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天氣 | 晴 | 雨 | 陰 | 陰 | 陰 | 雨 | 陰 | 晴 | 晴 | 晴 | 陰 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天氣 | 晴 | 陰 | 雨 | 陰 | 陰 | 晴 | 陰 | 晴 | 晴 | 晴 | 陰 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估計西安市在該天不下雨的概率;
(2)西安市某學校擬從4月份的一個晴天開始舉行連續2天的運動會,估計運動會期間不下雨的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A,B兩組各有7位病人,他們服用某種藥物后的康復時間(單位:天)記錄如下:
A組:10,11,12,13,14,15,16;
B組:12,13,15,16,17,14,![]() .
.
假設所有病人的康復時間相互獨立,從A,B兩組隨機各選1人,A組選出的人記為甲,B組選出的人記為乙.
(1)求甲的康復時間不少于14天的概率;
(2)如果![]() ,求甲的康復時間比乙的康復時間長的概率.
,求甲的康復時間比乙的康復時間長的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司對旗下的甲、乙兩個門店在1至9月份的營業額(單位:萬元)進行統計并得到如圖折線圖.

下面關于兩個門店營業額的分析中,錯誤的是( )
A.甲門店的營業額折線圖具有較好的對稱性,故而營業額的平均值約為32萬元
B.根據甲門店的營業額折線圖可知,該門店營業額的平均值在[20,25]內
C.根據乙門店的營業額折線圖可知,其營業額總體是上升趨勢
D.乙門店在這9個月份中的營業額的極差為25萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,網絡電商已經悄然進入了廣大市民的日常生活,并慢慢改變了人們的消費方式為了更好地服務民眾,某電商在其官方APP中設置了用戶評價反饋系統,以了解用戶對商品狀況和優惠活動的評價現從評價系統中隨機抽出200條較為詳細的評價信息進行統計,商品狀況和優惠活動評價的2×2列聯表如下:
對優惠活動好評 | 對優惠活動不滿意 | 合計 | |
對商品狀況好評 | 100 | 20 | 120 |
對商品狀況不滿意 | 50 | 30 | 80 |
合計 | 150 | 50 | 200 |
(I)能否在犯錯誤的概率不超過0.001的前提下認為優惠活動好評與商品狀況好評之間有關系?
(Ⅱ)為了回饋用戶,公司通過APP向用戶隨機派送每張面額為0元,1元,2元的三種優惠券用戶每次使用APP購物后,都可獲得一張優惠券,且購物一次獲得1元優惠券,2元優惠券的概率分別是![]() ,
,![]() ,各次獲取優惠券的結果相互獨立若某用戶一天使用了APP購物兩次,記該用戶當天獲得的優惠券面額之和為X,求隨機變量X的分布列和數學期望.
,各次獲取優惠券的結果相互獨立若某用戶一天使用了APP購物兩次,記該用戶當天獲得的優惠券面額之和為X,求隨機變量X的分布列和數學期望.
參考數據
P(K2≥k) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:K2![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
查看答案和解析>>
科目:高中數學 來源: 題型:
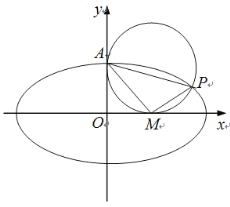
【題目】如圖,在平面直角坐標系xOy中,已知![]() 為橢圓
為橢圓![]() 的上頂點,P為橢圓E上異于上、下頂點的一個動點.當點P的橫坐標為
的上頂點,P為橢圓E上異于上、下頂點的一個動點.當點P的橫坐標為![]() 時,
時,![]() .
.
(1)求橢圓E的標準方程;
(2)設M為x軸的正半軸上的一個動點.
①若點P在第一象限內,且以AP為直徑的圓恰好與x軸相切于點M,求AP的長.
②若![]() ,是否存在點N,滿足
,是否存在點N,滿足![]() ,且AN的中點恰好在橢圓E上?若存在,求點N的坐標;若不存在,請說明理由.
,且AN的中點恰好在橢圓E上?若存在,求點N的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com