
【題目】下列說法正確的是( )
A. 命題“若x2=1,則x≠1”的否命題是“若x2=1,則x=1”
B. 命題“![]() ”的否定是“x∈R,x2﹣x>0”
”的否定是“x∈R,x2﹣x>0”
C. “y=f(x)在x0處有極值”是“f'(x0)=0”的充要條件
D. 命題“若函數f(x)=x2﹣ax+1有零點,則“a≥2或a≤﹣2”的逆否命題為真命題
【答案】D
【解析】
對于A,根據否命題的概念可得到結論;對于B特稱命題的否定是全稱命題;C,根據極值點的概念判斷即可;D,二次函數在R上有零點,即判別式大于等于0即可,可得到正誤.
對于A,命題“若x2=1,則x≠1”的否命題是“若x2≠1,則x=1”,否命題既否條件又否結論,故命題不正確;對于B,命題“![]() ”的否定是“x∈R,x2﹣x
”的否定是“x∈R,x2﹣x![]() 0”故命題錯誤;對于C,“y=f(x)在x0處有極值”,則“f'(x0)=0”,反之,“f'(x0)=0”不一定有“y=f(x)在x0處有極值”;對于D,命題“若函數f(x)=x2﹣ax+1有零點,則“a≥2或a≤﹣2”的逆否命題和原命題的真假性相同,原命題f(x)=x2﹣ax+1有零點,只需要判別式大于等于0,解得a的范圍即a≥2或a≤﹣2,是正確的,故逆否命題也是正確的。
0”故命題錯誤;對于C,“y=f(x)在x0處有極值”,則“f'(x0)=0”,反之,“f'(x0)=0”不一定有“y=f(x)在x0處有極值”;對于D,命題“若函數f(x)=x2﹣ax+1有零點,則“a≥2或a≤﹣2”的逆否命題和原命題的真假性相同,原命題f(x)=x2﹣ax+1有零點,只需要判別式大于等于0,解得a的范圍即a≥2或a≤﹣2,是正確的,故逆否命題也是正確的。
故答案為:D.


 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】某商場為了了解顧客的購物信息,隨機在商場收集了![]() 位顧客購物的相關數據如下表:
位顧客購物的相關數據如下表:
一次購物款(單位:元) |
|
|
|
|
|
顧客人數 |
|
|
|
|
|
統計結果顯示![]() 位顧客中購物款不低于
位顧客中購物款不低于![]() 元的顧客占
元的顧客占![]() ,該商場每日大約有
,該商場每日大約有![]() 名顧客,為了增加商場銷售額度,對一次購物不低于
名顧客,為了增加商場銷售額度,對一次購物不低于![]() 元的顧客發放紀念品.
元的顧客發放紀念品.
(Ⅰ)試確定![]() ,
, ![]() 的值,并估計每日應準備紀念品的數量;
的值,并估計每日應準備紀念品的數量;
(Ⅱ)現有![]() 人前去該商場購物,求獲得紀念品的數量
人前去該商場購物,求獲得紀念品的數量![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為圓
為圓![]() 的圓心,
的圓心, ![]() 是圓上的動點,點
是圓上的動點,點![]() 在圓的半徑
在圓的半徑![]() 上,且有點
上,且有點![]() 和
和![]() 上的點
上的點![]() ,滿足
,滿足![]() ,
, ![]() .
.
(1)當點![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡方程;
的軌跡方程;
(2)若斜率為![]() 的直線
的直線![]() 與圓
與圓![]() 相切,直線
相切,直線![]() 與(1)中所求點
與(1)中所求點![]() 的軌跡交于不同的兩點
的軌跡交于不同的兩點![]() ,
, ![]() ,
, ![]() 是坐標原點,且
是坐標原點,且![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a,b,c為實數,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).記集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若{S},{T}分別為集合S,T 的元素個數,則下列結論不可能的是( )
A.{S}=1且{T}=0B.{S}=1且{T}=1C.{S}=2且{T}=2D.{S}=2且{T}=3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒子內有3個不同的黑球,5個不同的白球.
(1)全部取出排成一列,3個黑球兩兩不相鄰的排法有多少種?
(2)從中任取6個球,白球的個數不比黑球個數少的取法有多少種?
(3)若取一個白球記2分,取一個黑球記1分,從中任取5個球,使總分不少于7分的取法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限x(年)和所支出的維修費用y萬元有如下的統計資料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)畫出散點圖并判斷是否線性相關;
(2)如果線性相關,求線性回歸方程;
(3)估計使用年限為10年時,維修費用是多少?
附注:①參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為 ;
;
②參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入4萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示),由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從0開始計數的.
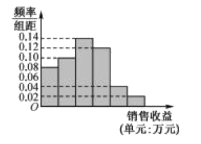
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司在若干地區各投入4萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 3 | 7 |
由表中的數據顯示,![]() 與
與![]() 之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出
之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出![]() 關于
關于![]() 的回歸直線方程.(參考公式:
的回歸直線方程.(參考公式: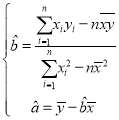 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
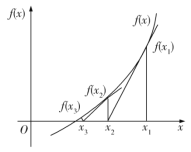
【題目】牛頓迭代法(Newton's method)又稱牛頓–拉夫遜方法(Newton–Raphsonmethod),是牛頓在17世紀提出的一種近似求方程根的方法.如圖,設![]() 是
是![]() 的根,選取
的根,選取![]() 作為
作為![]() 初始近似值,過點
初始近似值,過點![]() 作曲線
作曲線![]() 的切線
的切線![]() 與
與![]() 軸的交點的橫坐標
軸的交點的橫坐標![]() ,稱
,稱![]() 是
是![]() 的一次近似值,過點
的一次近似值,過點![]() 作曲線
作曲線![]() 的切線,則該切線與
的切線,則該切線與![]() 軸的交點的橫坐標為
軸的交點的橫坐標為![]() ,稱
,稱![]() 是
是![]() 的二次近似值.重復以上過程,直到
的二次近似值.重復以上過程,直到![]() 的近似值足夠小,即把
的近似值足夠小,即把![]() 作為
作為![]() 的近似解.設
的近似解.設![]() 構成數列
構成數列![]() .對于下列結論:
.對于下列結論:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中正確結論的序號為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com