
【題目】已知函數![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)討論![]() 的單調性;
的單調性;
(3)設![]() 、
、![]() 為曲線
為曲線![]() 上的任意兩點,并且
上的任意兩點,并且![]() ,若
,若![]() 恒成立,證明:
恒成立,證明:![]() .
.
【答案】(1)![]() ;(2)若
;(2)若![]() ,
, ![]() 在
在![]() 上遞增;若
上遞增;若![]() ,
,![]() 時,
時,![]() 單調遞增;
單調遞增;![]() ,
,![]() 單調遞減;(3)證明見解析.
單調遞減;(3)證明見解析.
【解析】
(1)將![]() 代入可得函數解析式,求得導數并代入
代入可得函數解析式,求得導數并代入![]() 求得切線的斜率.將
求得切線的斜率.將![]() 代入函數可得切點坐標,由點斜式即可求得切線方程.
代入函數可得切點坐標,由點斜式即可求得切線方程.
(2)先求得導函數,對![]() 分類討論,根據導函數的符號即可判斷單調性.
分類討論,根據導函數的符號即可判斷單調性.
(3)根據![]() 恒成立及(2)中函數單調性的討論,可求得
恒成立及(2)中函數單調性的討論,可求得![]() .代入函數并結合不等式即可得
.代入函數并結合不等式即可得![]() .利用定義作差,得
.利用定義作差,得![]() ,化簡后即可證明.
,化簡后即可證明.
(1)當![]() 時,
時,![]() ,
,
對函數![]() 求導得
求導得![]() ,
,
∴![]() ,又
,又![]() ,
,
∴曲線![]() 在
在![]() 處的切線方程為:
處的切線方程為:![]() ;
;
(2)求導得![]() ,
,
若![]() ,
,![]() ,
,![]() 在
在![]() 上遞增;
上遞增;
若![]() ,當
,當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() ,
,![]() 單調遞減.
單調遞減.
(3)由(2)知,若![]() ,
,![]() 在
在![]() 上遞增,
上遞增,
又![]() ,故
,故![]() 不恒成立.
不恒成立.
若![]() ,當
,當![]() 時,
時,![]() 遞減,
遞減,![]() ,不合題意.
,不合題意.
若![]() ,當
,當![]() 時,
時,![]() 遞增,
遞增,![]() ,不合題意.
,不合題意.
若![]() ,
,![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,![]() ,合題意.
,合題意.
故![]() ,且
,且![]() (當且僅當
(當且僅當![]() 時取“
時取“![]() ”).
”).
設![]() ,
,![]()
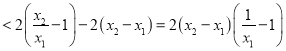 ,
,
∴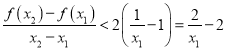 ,
,
因此,![]()
即![]()


科目:高中數學 來源: 題型:
【題目】下列命題中真命題的序號為(少填或錯填均不得分)______.若一個球的半徑縮小為原來的一半,則其體積縮小為原來的八分之一;②若兩組數據的平均值相等,則它們的標準差也相等;③直線![]() 與圓
與圓![]() 相切;④若兩個平面都垂直于同一個平面,則這兩個平面平行.
相切;④若兩個平面都垂直于同一個平面,則這兩個平面平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設計一個隨機試驗,使一個事件的概率與某個未知數有關,然后通過重復試驗,以頻率估計概率,即可求得未知數的近似解,這種隨機試驗在數學上稱為隨機模擬法,也稱為蒙特卡洛法。比如要計算一個正方形內部不規則圖形的面積,就可以利用撒豆子,計算出落在不規則圖形內部和正方形內部的豆子數比近似等于不規則圖形面積與正方形面積比,從而近似求出不規則圖形的面積.
統計學上還有一個非常著名的蒲豐投針實驗:平面上間隔![]() 的平行線,向平行線間的平面上任意投擲一枚長為
的平行線,向平行線間的平面上任意投擲一枚長為![]() 的針
的針![]() ,通過多次實驗可以近似求出針與任一平行線(以
,通過多次實驗可以近似求出針與任一平行線(以![]() 為例)相交(當針的中點在平行線外不算相交)的概率.以
為例)相交(當針的中點在平行線外不算相交)的概率.以![]() 表示針的中點與最近一條平行線
表示針的中點與最近一條平行線![]() 的距離,又以
的距離,又以![]() 表示
表示![]() 與
與![]() 所成夾角,如圖甲,易知滿足條件:
所成夾角,如圖甲,易知滿足條件:![]() ,
,![]() .
.
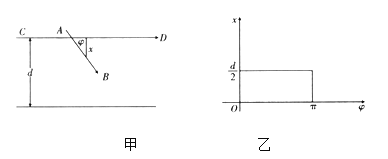
由這兩式可以確定平面上的一個矩形![]() ,如圖乙,在圖甲中,當
,如圖乙,在圖甲中,當![]() 滿足___________(
滿足___________(![]() 與
與![]() ,
,![]() 之間的關系)時,針與平行線相交(記為事件
之間的關系)時,針與平行線相交(記為事件![]() ).可用從實驗中獲得的頻率去近似
).可用從實驗中獲得的頻率去近似![]() ,即投針
,即投針![]() 次,其中相交的次數為
次,其中相交的次數為![]() ,則
,則![]() ,歷史上有一個數學家親自做了這實驗,他投擲的次數是5000,相交的次數為2550次,
,歷史上有一個數學家親自做了這實驗,他投擲的次數是5000,相交的次數為2550次,![]() ,
,![]() ,依據這個實驗求圓周率
,依據這個實驗求圓周率![]() 的近似值_________.(精確到3位小數)
的近似值_________.(精確到3位小數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 滿足:對一切
滿足:對一切![]() ,有
,有![]() ,其中
,其中![]() 是與
是與![]() 無關的常數,稱數列上有界(有上界),并稱
無關的常數,稱數列上有界(有上界),并稱![]() 是它的一個上界,對一切
是它的一個上界,對一切![]() ,有
,有![]() ,其中
,其中![]() 是與
是與![]() 無關的常數,稱數列下有界(有下界),并稱
無關的常數,稱數列下有界(有下界),并稱![]() 是它的一個下界.一個數列既有上界又有下界,則稱為有界數列,常值數列是一個特殊的有界數列.設
是它的一個下界.一個數列既有上界又有下界,則稱為有界數列,常值數列是一個特殊的有界數列.設![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,
,![]() .
.
(1)若數列![]() 為常數列,試求實數
為常數列,試求實數![]() 、
、![]() 滿足的等式關系,并求出實數
滿足的等式關系,并求出實數![]() 的取值范圍;
的取值范圍;
(2)下面四個選項,對一切實數![]() ,恒正確的是.(寫出所有正確選項,不需要證明其正確,但需要簡單說明一下為什么不選余下幾個)
,恒正確的是.(寫出所有正確選項,不需要證明其正確,但需要簡單說明一下為什么不選余下幾個)
A. 當![]() 時,
時,![]() B. 當
B. 當![]() 時,
時,![]()
C. 當![]() 時,
時,![]() D. 當
D. 當![]() 時,
時,![]()
(3)若![]() ,
,![]() ,且數列
,且數列![]() 是有界數列,求
是有界數列,求![]() 的值及
的值及![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極點為直角坐標系的原點,極軸為![]() 軸正半軸且單位長度相同的極坐標系中曲線
軸正半軸且單位長度相同的極坐標系中曲線![]() ,
,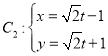 (
(![]() 為參數).
為參數).
(Ⅰ)求曲線![]() 上的點到曲線
上的點到曲線![]() 距離的最小值;
距離的最小值;
(Ⅱ)若把![]() 上各點的橫坐標都擴大原來為原來的2倍,縱坐標擴大原來的
上各點的橫坐標都擴大原來為原來的2倍,縱坐標擴大原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設
,設![]() ,曲線
,曲線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com