
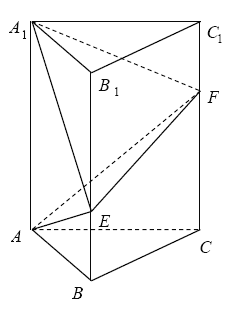
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,點E,F分別在
,點E,F分別在![]() ,
,![]() ,且
,且![]() ,
,![]() .設
.設![]() .
.
(1)當![]() 時,求異面直線
時,求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(2)當平面![]() 平面
平面![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)60°(2)![]()
【解析】
(1)推導出![]() 平面ABC,
平面ABC,![]() AC,建立分別以AB,AC,
AC,建立分別以AB,AC,![]() 為
為![]() 軸的空間直角坐標系,利用法向量能求出異面直線AE與
軸的空間直角坐標系,利用法向量能求出異面直線AE與![]() 所成角.
所成角.
(2)推導出平面![]() 的法向量和平面
的法向量和平面![]() 的一個法向量,由平面
的一個法向量,由平面![]() 平面
平面![]() ,能求出
,能求出![]() 的值.
的值.
解:因為直三棱柱![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
又因為![]() ,
,
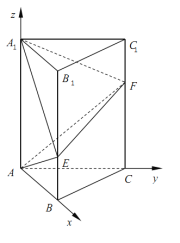
所以建立分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸的空間直角坐標系
軸的空間直角坐標系![]() .
.
(1)設![]() ,則
,則![]() ,
,![]() ,
,
各點的坐標為![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
因為![]() ,
,![]() ,
,
所以 .
.
所以向量![]() 和
和![]() 所成的角為120°,
所成的角為120°,
所以異面直線![]() 與
與![]() 所成角為60°;
所成角為60°;
(2)因為![]() ,
,![]() ,
,
![]() ,
,![]()
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,且
,且![]() .
.
即![]() ,且
,且![]() .
.
令![]() ,則
,則![]() ,
,![]() .
.
所以![]() 是平面
是平面![]() 的一個法向量.
的一個法向量.
同理,![]() 是平面
是平面![]() 的一個法向量.
的一個法向量.
因為平面![]() 平面
平面![]() ,
,
所以![]() ,
,
![]() ,
,
解得![]() .
.
所以當平面![]() 平面
平面![]() 時,
時,![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】新能源汽車是我國汽車工業由大變強的一條必經之路!國家對其給予政策上的扶持,己成為我國的戰略方針.近年來,我國新能源汽車制造蓬勃發展,某著名車企自主創新,研發了一款新能源汽車,經過大數據分析獲得:在某種路面上,該品牌汽車的剎車距離![]() (米)與其車速
(米)與其車速![]() (千米/小時)滿足下列關系:
(千米/小時)滿足下列關系:![]() (
(![]() ,
,![]() 是常數).(行駛中的新能源汽車在剎車時由于慣性作用,要繼續往前滑行一段距離才能停下,這段距離叫做剎車距離).如圖是根據多次對該新能源汽車的實驗數據繪制的剎車距離
是常數).(行駛中的新能源汽車在剎車時由于慣性作用,要繼續往前滑行一段距離才能停下,這段距離叫做剎車距離).如圖是根據多次對該新能源汽車的實驗數據繪制的剎車距離![]() (米)與該車的車速
(米)與該車的車速![]() (千米/小時)的關系圖.該新能源汽車銷售公司為滿足市場需求,國慶期間在甲、乙兩地同時展銷該品牌的新能源汽車,在甲地的銷售利潤(單位:萬元)為
(千米/小時)的關系圖.該新能源汽車銷售公司為滿足市場需求,國慶期間在甲、乙兩地同時展銷該品牌的新能源汽車,在甲地的銷售利潤(單位:萬元)為![]() ,在乙地的銷售利潤(單位:萬元)為
,在乙地的銷售利潤(單位:萬元)為![]() ,其中
,其中![]() 為銷售量(單位:輛).
為銷售量(單位:輛).
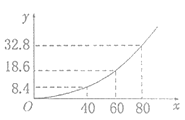
(1)若該公司在兩地共銷售20輛該品牌的新能源汽車,則能獲得的最大利潤![]() 是多少?
是多少?
(2)如果要求剎車距離不超過25.2米,求該品牌新能源汽車行駛的最大速度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面為正方形的四棱錐P-ABCD中,側棱PD⊥底面ABCD,PD=DC,點E是線段PC的中點.

(1)求異面直線AP與BE所成角的大小;
(2)若點F在線段PB上,使得二面角F-DE-B的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義城為D,若滿足條件:存在
的定義城為D,若滿足條件:存在![]() ,使
,使![]() 在
在![]() 上的值城為
上的值城為![]() (
(![]() 且
且![]() ),則稱
),則稱![]() 為“k倍函數”,給出下列結論:①
為“k倍函數”,給出下列結論:①![]() 是“1倍函數”;②
是“1倍函數”;②![]() 是“2倍函數”:③
是“2倍函數”:③![]() 是“3倍函數”.其中正確的是( )
是“3倍函數”.其中正確的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
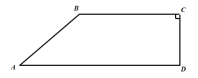
【題目】如圖,某山地車訓練中心有一直角梯形森林區域![]() ,其四條邊均為道路,其中
,其四條邊均為道路,其中![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.現有甲、乙兩名特訓隊員進行野外對抗訓練,要求同時從
千米.現有甲、乙兩名特訓隊員進行野外對抗訓練,要求同時從![]() 地出發勻速前往
地出發勻速前往![]() 地,其中甲的行駛路線是
地,其中甲的行駛路線是![]() ,速度為
,速度為![]() 千米/小時,乙的行駛路線是
千米/小時,乙的行駛路線是![]() ,速度為
,速度為![]() 千米/小時.
千米/小時.
(1)若甲、乙兩名特訓隊員到達![]() 地的時間相差不超過
地的時間相差不超過![]() 分鐘,求乙的速度
分鐘,求乙的速度![]() 的取值范圍;
的取值范圍;
(2)已知甲、乙兩名特訓隊員攜帶的無線通訊設備有效聯系的最大距離是![]() 千米.若乙先于甲到達
千米.若乙先于甲到達![]() 地,且乙從
地,且乙從![]() 地到
地到![]() 地的整個過程中始終能用通訊設備對甲保持有效聯系,求乙的速度
地的整個過程中始終能用通訊設備對甲保持有效聯系,求乙的速度![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2014年12月19日,2014年中國數學奧林匹克競賽(第30屆全國中學生數學冬令營)在重慶市巴蜀中學舉行.參加本屆中國數學奧林匹克競賽共有來自各省、市(自治區、直轄市)、香港地區、澳門地區,以及俄羅斯、新加坡等國的30余支代表隊,共317名選手.競賽為期2天,每天3道題,限時4個半小時完成.部分優勝者將參加為國際數學奧林匹克競賽而組建的中國國家集訓隊.中國數學奧林匹克競賽(全國中學生數學冬令營)是在全國高中數學聯賽基礎上進行的一次較高層次的數學競賽,該項活動也是中國中學生級別最高、規模最大、最有影響的全國性數學競賽.2020年第29屆全國中學生生物學競賽也將在重慶巴蜀中學舉行.巴蜀中學校本選修課“數學建模”興趣小組調查了2019年參加全國生物競賽的200名學生(其中男生、女生各100人)的成績,得到這200名學生成績的中位數為78.這200名學生成績均在50與110之間,且成績在![]() 內的人數為30,這200名學生成績的高于平均數的男生有62名,女生有38名.并根據調查結果畫出如圖所示的頻率分布直方圖.
內的人數為30,這200名學生成績的高于平均數的男生有62名,女生有38名.并根據調查結果畫出如圖所示的頻率分布直方圖.
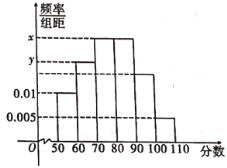
(1)求![]() ,
,![]() 的值;
的值;
(2)填寫下表,能否有![]() 的把握認為學生成績是否高于平均數與性別有關系?
的把握認為學生成績是否高于平均數與性別有關系?
男生 | 女生 | 總計 | |
成績不高于平均數 | |||
成績高于平均數 | |||
總計 |
參考公式及數據: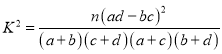 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是橢圓
是橢圓![]() 上的點,
上的點,![]() ,
,![]() 是焦點,離心率
是焦點,離心率![]() .
.
(1)求橢圓的方程;
(2)設![]() ,
,![]() 是橢圓上的兩點,且
是橢圓上的兩點,且![]() ,(
,(![]() 是定數),問線段
是定數),問線段![]() 的垂直平分線是否過定點?若過定點,求出此定點的坐標,若不存在,說明理由.
的垂直平分線是否過定點?若過定點,求出此定點的坐標,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com