
【題目】已知函數![]() 且在
且在![]() 上的最大值為
上的最大值為![]() ,
,
(1)求函數f(x)的解析式;
(2)判斷函數f(x)在(0,π)內的零點個數,并加以證明
【答案】(1)![]() (2)2個零點.
(2)2個零點.
【解析】
(1)由題意,可借助導數研究函數![]() 上的單調性,確定出最值,令最值等于
上的單調性,確定出最值,令最值等于![]() ,即可得到關于a的方程,由于a的符號對函數的最值有影響,故可以對a的取值范圍進行討論,分類求解;(2)借助導數研究函數f(x)在(0,π)內單調性,由零點判定定理即可得出零點的個數.
,即可得到關于a的方程,由于a的符號對函數的最值有影響,故可以對a的取值范圍進行討論,分類求解;(2)借助導數研究函數f(x)在(0,π)內單調性,由零點判定定理即可得出零點的個數.
(1)由已知得f′(x)=a(sinx+xcosx),對于任意的x∈(0, ![]() ),
),
有sinx+xcosx>0,當a=0時,f(x)= ![]() ,不合題意;
,不合題意;
當a<0時,x∈(0,![]() ),f′(x)<0,從而f(x)在(0,
),f′(x)<0,從而f(x)在(0, ![]() )單調遞減,
)單調遞減,
又函數f(x)=axsinx![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上圖象是連續不斷的,
]上圖象是連續不斷的,
故函數在[0, ![]() ]上的最大值為f(0),不合題意;
]上的最大值為f(0),不合題意;
當a>0時,x∈(0, ![]() ),f′(x)>0,從而f(x)在(0,
),f′(x)>0,從而f(x)在(0, ![]() )單調遞增,
)單調遞增,
又函數f(x)=axsinx ![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上圖象是連續不斷的,
]上圖象是連續不斷的,
故函數在[0, ![]() ]上上的最大值為f(
]上上的最大值為f(![]() )=
)=![]() a
a![]() =
=![]() ,解得a=1,
,解得a=1,
綜上所述,得![]() ;
;
(2)函數f(
由(I)知,f(x)=xsinx![]() ,從而有f(0)=
,從而有f(0)= ![]() <0,f(
<0,f(![]() )=π32>0,
)=π32>0,
又函數在[0, ![]() ]上圖象是連續不斷的,所以函數f(x)在(0,
]上圖象是連續不斷的,所以函數f(x)在(0, ![]() )內至少存在一個零點,
)內至少存在一個零點,
又由(I)知f(x)在(0, ![]() )單調遞增,故函數f(x)在(0,
)單調遞增,故函數f(x)在(0, ![]() )內僅有一個零點。
)內僅有一個零點。
當x∈[![]() ,π]時,令g(x)=f′(x)=sinx+xcosx,
,π]時,令g(x)=f′(x)=sinx+xcosx,
由g(![]() )=1>0,g(π)=π<0,且g(x)在[
)=1>0,g(π)=π<0,且g(x)在[![]() ,π]上的圖象是連續不斷的,
,π]上的圖象是連續不斷的,
故存在m∈![]() ,π),使得g(m)=0.
,π),使得g(m)=0.
由g′(x)=2cosxxsinx,知x∈(![]() ,π)時,有g′(x)<0,
,π)時,有g′(x)<0,
從而g(x)在[![]() ,π]上單調遞減。
,π]上單調遞減。
當x∈![]() ,m),g(x)>g(m)=0,即f′(x)>0,
,m),g(x)>g(m)=0,即f′(x)>0,
從而f(x)在(![]() ,m)內單調遞增
,m)內單調遞增
故當x∈(![]() ,m)時,f(x)>f(π2)=π32>0,
,m)時,f(x)>f(π2)=π32>0,
從而(x)在(![]() ,m)內無零點;
,m)內無零點;
當x∈(m,π)時,有g(x)<g(m)=0,即f′(x)<0,
從而f(x)在(![]() ,m)內單調遞減。
,m)內單調遞減。
又f(m)>0,f(π)<0且f(x)在[m,π]上的圖象是連續不斷的,
從而f(x)在[m,π]內有且僅有一個零點。
綜上所述,函數f(x)在(0,π)內有且僅有兩個零點。


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸,取相同的單位長度建立極坐標系.
軸的非負半軸為極軸,取相同的單位長度建立極坐標系.
(1)求圓![]() 的普通方程及其極坐標方程;
的普通方程及其極坐標方程;
(2)設直線![]() 的極坐標方程為
的極坐標方程為![]() ,射線
,射線![]() 與圓
與圓![]() 的交點為
的交點為![]() (異于極點),與直線
(異于極點),與直線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公比大于
是公比大于![]() 的等比數列,
的等比數列,![]() 為數列
為數列![]() 的前
的前![]() 項和,
項和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差數列.數列
成等差數列.數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() 滿足
滿足![]() ,且
,且![]() ,
,
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)令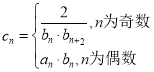 ,求數列
,求數列![]() 的前
的前![]() 項和為
項和為![]() ;
;
(3)將數列![]() ,
,![]() 的項按照“當
的項按照“當![]() 為奇數時,
為奇數時,![]() 放在前面;當
放在前面;當![]() 為偶數時,
為偶數時,![]() 放在前面”的要求進行排列,得到一個新的數列:
放在前面”的要求進行排列,得到一個新的數列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求這個新數列的前
,求這個新數列的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用一個長為![]() ,寬為
,寬為![]() 的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
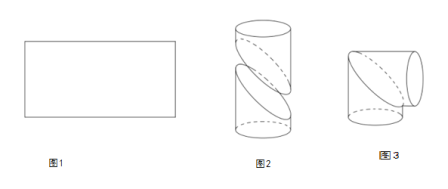
(1)求直角圓形彎管(圖3)的體積;
(2)求斜截面橢圓的焦距;
(3)在相應的圖1中建立適當的坐標系,使所畫的曲線的方程為![]() ,求出方程并畫出大致圖像;
,求出方程并畫出大致圖像;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線l的參數方程為:
,直線l的參數方程為:![]() (t為參數),直線l與曲線C分別交于
(t為參數),直線l與曲線C分別交于![]() 兩點.
兩點.
(1)寫出曲線C和直線l的普通方程;
(2)若點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由無理數引發的數學危機一直延續到19世紀,直到1872年,德國數學家戴德金提出了“戴德金分割”,才結束了持續2000多年的數學史上的第一次大危機.所謂戴德金分割,是指將有理數集![]() 劃分為兩個非空的子集
劃分為兩個非空的子集![]() 與
與![]() ,且滿足
,且滿足![]() ,
,![]() ,
,![]() 中的每一個元素都小于
中的每一個元素都小于![]() 中的每一個元素,則稱
中的每一個元素,則稱![]() 為戴德金分割.試判斷,對于任一戴德金分割
為戴德金分割.試判斷,對于任一戴德金分割![]() ,下列選項中不可能成立的是
,下列選項中不可能成立的是
A.![]() 沒有最大元素,
沒有最大元素,![]() 有一個最小元素
有一個最小元素
B.![]() 沒有最大元素,
沒有最大元素,![]() 也沒有最小元素
也沒有最小元素
C.![]() 有一個最大元素,
有一個最大元素,![]() 有一個最小元素
有一個最小元素
D.![]() 有一個最大元素,
有一個最大元素,![]() 沒有最小元素
沒有最小元素
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com