
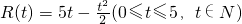 (單位:萬元),其中t(t∈N)是產品售出的數量(單位:百件)
(單位:萬元),其中t(t∈N)是產品售出的數量(單位:百件)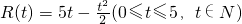 ,
, -0.5-0.25x=-0.5+4.75x-
-0.5-0.25x=-0.5+4.75x- ,
, -0.5-0.25x=12-0.25x,
-0.5-0.25x=12-0.25x,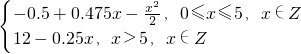 .
. ,
, ≥0,得0≤x≤5,x∈Z;
≥0,得0≤x≤5,x∈Z;

科目:高中數學 來源: 題型:單選題
 ),則f(x)在定義域內是
),則f(x)在定義域內是查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,開始時桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指數衰減曲線y1=a•e-nt(n為常數,t為注水時間),那么桶2中的水就是y2=a-a•e-nt.如果由桶1向桶2中注水5分鐘時,兩桶中的水相等,那么經過________分鐘桶1中的水只有
如圖,開始時桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指數衰減曲線y1=a•e-nt(n為常數,t為注水時間),那么桶2中的水就是y2=a-a•e-nt.如果由桶1向桶2中注水5分鐘時,兩桶中的水相等,那么經過________分鐘桶1中的水只有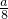 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com