Question

1．邊長為1的等邊三角形ABC中，沿BC邊高線AD折起，使得折后二面角B-AD-C為60°，點D到平面ABC的距離為$\frac{\sqrt{15}}{10}$．

Answer 1

分析 根據條件確定AE為點A到直線BC的距離，DH為點D到面ABC的距離，然后利用邊長關系進行求值即可．

解答 解：如圖，過D點作DE⊥BC，連AE，則AE⊥BC，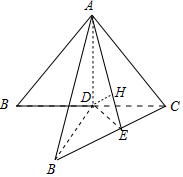
∴AE為點A到直線BC的距離，
在直角三角形ADE中，AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{（\frac{\sqrt{3}}{2}）^{2}+（\frac{\sqrt{3}}{4}）^{2}}=\frac{\sqrt{15}}{4}$．
又BC面ADE，且BC?面ABC，
∴面ABC⊥面ADE，AE為高線，作DH⊥AE于H，則DH⊥面ABC，
∴DH為點D到面ABC的距離，
由DH•AE=AD•DE，得DH=$\frac{\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{4}}{\frac{\sqrt{15}}{4}}$=$\frac{\sqrt{15}}{10}$．
故答案為：$\frac{\sqrt{15}}{10}$．

點評 本題主要考查空間點到直線和點到平面的距離，利用距離公式進行求解，考查學生的運算能力，是中檔題．