
分析 (I)由點Pn(n,Sn)都在函數f(x)=x2+2x的圖象上,可得Sn=n2+2n,利用遞推關系可得an.
(II)f′(x)=2x+2,過點Pn(n,Sn)的切線的斜率為k.可得kn=2n+2.bn=$\frac{1}{{a}_{n}•({k}_{n}+1)}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$,再利用“裂項求和”方法即可得出.
解答 解:(I)∵點Pn(n,Sn)都在函數f(x)=x2+2x的圖象上,∴Sn=n2+2n,
n=1時,a1=3;n≥2,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1.
當n=1時上式也成立,∴an=2n+1.
(II)f′(x)=2x+2,過點Pn(n,Sn)的切線的斜率為k.
∴kn=2n+2.∴bn=$\frac{1}{{a}_{n}•({k}_{n}+1)}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$,
∴數列{bn}的前n項和Tn=$\frac{1}{2}[(\frac{1}{3}-\frac{1}{5})$+$(\frac{1}{5}-\frac{1}{7})$+…+$(\frac{1}{2n+1}-\frac{1}{2n+3})]$
=$\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+3})$=$\frac{n}{6n+9}$.
點評 本題考查了等差數列與等比數列的通項公式與求和公式、數列遞推關系、“裂項求和”方法、導數的幾何意義、函數的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
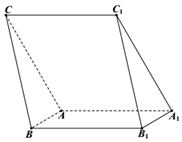 如圖,三棱柱ABC-A1B1C1中,側面ACC1A1⊥側面ABB1A1,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=1.
如圖,三棱柱ABC-A1B1C1中,側面ACC1A1⊥側面ABB1A1,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
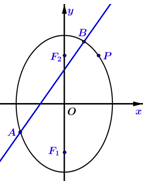 設橢圓$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)經過點$P(1,\sqrt{2})$,其離心率與雙曲線x2-y2=1的離心率互為倒數.
設橢圓$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)經過點$P(1,\sqrt{2})$,其離心率與雙曲線x2-y2=1的離心率互為倒數.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com