
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,橢圓的離心率為
,橢圓的離心率為![]() ,過橢圓
,過橢圓![]() 的左焦點
的左焦點![]() ,且斜率為
,且斜率為![]() 的直線
的直線![]() ,與以右焦點
,與以右焦點![]() 為圓心,半徑為
為圓心,半徑為![]() 的圓
的圓![]() 相切.
相切.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)線段![]() 是橢圓
是橢圓![]() 過右焦點
過右焦點![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面積的最大值以及取最大值時實數
的面積的最大值以及取最大值時實數![]() 的值.
的值.
【答案】(1)![]() (2)最大值
(2)最大值![]() ,
,![]() .
.
【解析】
(1)設![]() ,
,![]() ,可得:直線
,可得:直線![]() 的方程為:
的方程為:![]() ,即
,即![]() ,直線
,直線![]() 與圓
與圓![]() 相切,圓心
相切,圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,解得
,解得![]() ,結合已知,即可求得答案.
,結合已知,即可求得答案.
(2)將直線![]() 的方程與橢圓方程聯立,求得
的方程與橢圓方程聯立,求得![]() ,結合導數知識,即可求得答案.
,結合導數知識,即可求得答案.
(1)設![]() ,
,![]() ,
,
![]() 直線
直線![]() 斜率為
斜率為![]() ,且過橢圓
,且過橢圓![]() 的左焦點
的左焦點![]() .
.
![]() 直線
直線![]() 的方程為:
的方程為:![]() ,即
,即![]() .
.
![]() 直線
直線![]() 與圓
與圓![]() 相切,
相切,
![]() 圓心
圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
解得![]() .
.
![]() 橢圓
橢圓![]() 的離心率為
的離心率為![]() ,即
,即![]() ,
,
解得:![]() ,
,
根據:![]()
![]() 橢圓
橢圓![]() 的方程為
的方程為![]() .
.
(2)由(1)得![]() ,
,![]() ,
,
![]()
![]()
![]() 直線
直線![]() 的斜率不為
的斜率不為![]() ,
,
![]() 設直線
設直線![]() 的方程為:
的方程為:![]() ,
,
將直線![]() 的方程與橢圓方程聯立可得:
的方程與橢圓方程聯立可得: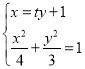 消掉
消掉![]()
可得:![]() ,
,
![]() 恒成立,
恒成立,
設![]() ,
,![]() ,
,
則![]() ,
,![]() 是上述方程的兩個不等根,
是上述方程的兩個不等根,
根據韋達定理可得:
![]() ,
,![]() .
.
![]() 的面積:
的面積:![]()
![]()
![]()
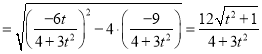
設![]() ,則
,則![]() ,
,![]() ,
,
![]()
![]()
可得:![]() .
.
令![]()
![]()
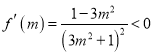 恒成立,
恒成立,
![]() 函數
函數![]() 在
在![]() 上為減函數,故
上為減函數,故![]() 的最大值為:
的最大值為:![]() ,
,
![]()
![]() 的面積的最大值為
的面積的最大值為![]() ,
,
當且僅當![]() ,即
,即![]() 時取最大值,
時取最大值,
此時直線![]() 的方程為
的方程為![]() ,即直線
,即直線![]() 垂直于
垂直于![]() 軸,
軸,
此時![]() ,即
,即![]() .
.
綜上所述,![]() 的面積的最大值
的面積的最大值![]() ,
,![]() 時
時![]() 的面積的最大.
的面積的最大.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】給出下列說法:
①“![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
②定義在![]() 上的偶函數
上的偶函數![]() 的最大值為30;
的最大值為30;
③命題“![]() ,
,![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ”.其中正確說法的個數為
”.其中正確說法的個數為
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知復數z滿足|z|![]() ,z的實部大于0,z2的虛部為2.
,z的實部大于0,z2的虛部為2.
(1)求復數z;
(2)設復數z,z2,z﹣z2之在復平面上對應的點分別為A,B,C,求(![]() )
)![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)已知射線![]() ,若
,若![]() 與圓
與圓![]() 交于點
交于點![]() (異于點
(異于點![]() ),
),![]() 與直線
與直線![]() 交于點
交于點![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,上頂點為
,上頂點為![]() ,過點
,過點![]() 與
與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于點
軸負半軸于點![]() ,且
,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右焦點
的右焦點![]() 作斜率為1的直線
作斜率為1的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,試在
兩點,試在![]() 軸上求一點
軸上求一點![]() ,使得以
,使得以![]() ,
,![]() 為鄰邊的平行四邊形是菱形.
為鄰邊的平行四邊形是菱形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】比較甲、乙兩名學生的數學學科素養的各項能力指標值(滿分為5分,分值高者為優),繪制了如圖1所示的六維能力雷達圖,例如圖中甲的數學抽象指標值為4,乙的數學抽象指標值為5,則下面敘述正確的是( )
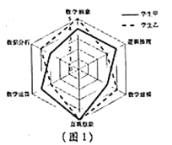
A. 乙的邏輯推理能力優于甲的邏輯推理能力
B. 甲的數學建模能力指標值優于乙的直觀想象能力指標值
C. 乙的六維能力指標值整體水平優于甲的六維能力指標值整體水平
D. 甲的數學運算能力指標值優于甲的直觀想象能力指標值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】10月1日,某品牌的兩款最新手機(記為![]() 型號,
型號,![]() 型號)同時投放市場,手機廠商為了解這兩款手機的銷售情況,在10月1日當天,隨機調查了5個手機店中這兩款手機的銷量(單位:部),得到下表:
型號)同時投放市場,手機廠商為了解這兩款手機的銷售情況,在10月1日當天,隨機調查了5個手機店中這兩款手機的銷量(單位:部),得到下表:
手機店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
(Ⅰ)若在10月1日當天,從![]() ,
,![]() 這兩個手機店售出的新款手機中各隨機抽取1部,求抽取的2部手機中至少有一部為
這兩個手機店售出的新款手機中各隨機抽取1部,求抽取的2部手機中至少有一部為![]() 型號手機的概率;
型號手機的概率;
(Ⅱ)現從這5個手機店中任選3個舉行促銷活動,用![]() 型號手機銷量超過
型號手機銷量超過![]() 型號手機銷量的手機店的個數,求隨機變量
型號手機銷量的手機店的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(III)經測算,![]() 型號手機的銷售成本
型號手機的銷售成本![]() (百元)與銷量(部)滿足關系
(百元)與銷量(部)滿足關系![]() .若表中
.若表中![]() 型號手機銷量的方差
型號手機銷量的方差![]() ,試給出表中5個手機店的
,試給出表中5個手機店的![]() 型號手機銷售成本的方差
型號手機銷售成本的方差![]() 的值.(用
的值.(用![]() 表示,結論不要求證明)
表示,結論不要求證明)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com