Question

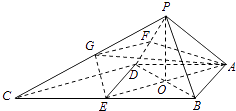
【題目】如圖，四棱錐P﹣ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB與△PAD都是等邊三角形．

（1）證明：PB⊥CD；
（2）求二面角A﹣PD﹣C的大小．

Answer 1

【答案】
（1）證明：取BC的中點E，連接DE，可得四邊形ABED是正方形

過點P作PO⊥平面ABCD，垂足為O，連接OA、OB、OD、OE

∵△PAB與△PAD都是等邊三角形，∴PA=PB=PD，可得OA=OB=OD

因此，O是正方形ABED的對角線的交點，可得OE⊥OB

∵PO⊥平面ABCD，得直線OB是直線PB在內的射影，∴OE⊥PB

∵△BCD中，E、O分別為BC、BD的中點，∴OE∥CD，可得PB⊥CD；

（2）解：由（1）知CD⊥PO，CD⊥PB

∵PO、PB是平面PBD內的相交直線，∴CD⊥平面PBD

∵PD平面PBD，∴CD⊥PD

取PD的中點F，PC的中點G，連接FG，

則FG為△PCD有中位線，∴FG∥CD，可得FG⊥PD

連接AF，由△PAD是等邊三角形可得AF⊥PD，∴∠AFG為二面角A﹣PD﹣C的平面角

連接AG、EG，則EG∥PB

∵PB⊥OE，∴EG⊥OE，

設AB=2，則AE=2 ，EG= PB=1，故AG= =3

在△AFG中，FG= CD= ，AF= ，AG=3

∴cos∠AFG= =﹣ ，得∠AFG=π﹣arccos ，

即二面角A﹣PD﹣C的平面角大小是π﹣arccos ．

【解析】（1）取BC的中點E，連接DE，過點P作PO⊥平面ABCD于O，連接OA、OB、OD、OE．可證出四邊形ABED是正方形，且O為正方形ABED的中心．因此OE⊥OB，結合三垂線定理，證出OE⊥PB，而OE是△BCD的中位線，可得OE∥CD，因此PB⊥CD；（2）由（1）的結論，證出CD⊥平面PBD，從而得到CD⊥PD．取PD的中點F，PC的中點G，連接FG，可得FG∥CD，所以FG⊥PD．連接AF，可得AF⊥PD，因此∠AFG為二面角A﹣PD﹣C的平面角，連接AG、EG，則EG∥PB，可得EG⊥OE．設AB=2，可求出AE、EG、AG、AF和FG的長，最后在△AFG中利用余弦定理，算出∠AFG=π﹣arccos ，即得二面角A﹣PD﹣C的平面角大小．
【考點精析】本題主要考查了直線與平面垂直的性質和共線向量與共面向量的相關知識點，需要掌握垂直于同一個平面的兩條直線平行；向量共線的充要條件：對于空間任意兩個向量，，的充要條件是存在實數，使才能正確解答此題．