
【題目】設f(x)是定義在實數集R上的函數,滿足條件y=f(x+1)是偶函數,且當x≥1時,f(x)= ![]() ,則
,則 ![]() 的大小關系是( )
的大小關系是( )
A.![]()
B.![]()
C.![]()
D.![]()
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設甲、乙兩人每次射擊命中目標的概率分別為 ![]() ,且各次射擊相互獨立,若按甲、乙、甲、乙…的次序輪流射擊,直到有一人擊中目標就停止射擊,則停止射擊時,甲射擊了兩次的概率是( )
,且各次射擊相互獨立,若按甲、乙、甲、乙…的次序輪流射擊,直到有一人擊中目標就停止射擊,則停止射擊時,甲射擊了兩次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M為線段AD上一點,AM=2MD,N為PC的中點.
(1)證明:MN∥平面PAB;
(2)求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“過大年,吃水餃”是我國不少地方過春節的一大習俗.2018年春節前夕, ![]() 市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標,
市某質檢部門隨機抽取了100包某種品牌的速凍水餃,檢測其某項質量指標,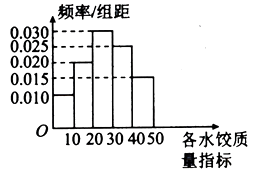
(1)求所抽取的100包速凍水餃該項質量指標值的樣本平均數 ![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)①由直方圖可以認為,速凍水餃的該項質量指標值 ![]() 服從正態分布
服從正態分布 ![]() ,利用該正態分布,求
,利用該正態分布,求 ![]() 落在
落在 ![]() 內的概率;
內的概率;
②將頻率視為概率,若某人從某超市購買了4包這種品牌的速凍水餃,記這4包速凍水餃中這種質量指標值位于 ![]() 內的包數為
內的包數為 ![]() ,求
,求 ![]() 的分布列和數學期望.
的分布列和數學期望.
附:①計算得所抽查的這100包速凍水餃的質量指標的標準差為 ![]() ;
;
②若 ![]() ,則
,則 ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 點(n,Sn+3)(n∈N*)在函數y=3×2x的圖象上,等比數列{bn}滿足bn+bn+1=an(n∈N*).其前n項和為Tn , 則下列結論正確的是( )
A.Sn=2Tn
B.Tn=2bn+1
C.Tn>an
D.Tn<bn+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex-e-x(x∈R,且e為自然對數的底數).
(1)判斷函數f(x)的單調性與奇偶性;
(2)是否存在實數t , 使不等式f(x-t)+f(x2-t2)≥0對一切x∈R都成立?若存在,求出t;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知坐標平面上動點 ![]() 與兩個定點
與兩個定點 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求點 ![]() 的軌跡方程,并說明軌跡是什么圖形;
的軌跡方程,并說明軌跡是什么圖形;
(2)記(1)中軌跡為 ![]() ,過點
,過點 ![]() 的直線
的直線 ![]() 被
被 ![]() 所截得的線段長度為8,求直線
所截得的線段長度為8,求直線 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() ,
, ![]() ,設
,設 ![]() .
.
(Ⅰ)若f(α)=2,求 ![]() 的值;
的值;
(Ⅱ)在△ABC中,角A,B,C的對邊分別是a,b,c,且滿足(2a﹣b)cosC=ccosB,求f(A)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠為預測產品的回收率 ![]() ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量 ![]() 之間的相關關系,現收集了4組對照數據。
之間的相關關系,現收集了4組對照數據。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)請根據相關系數 ![]() 的大小判斷回收率
的大小判斷回收率 ![]() 與
與 ![]() 之間是否存在高度線性相關關系;
之間是否存在高度線性相關關系;
(Ⅱ)請根據上表提供的數據,用最小二乘法求出 ![]() 關于
關于 ![]() 的線性回歸方程
的線性回歸方程 ![]() ,并預測當
,并預測當 ![]() 時回收率
時回收率 ![]() 的值.
的值.
參考數據: 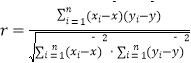
| 1 | 0 |
|
| 其他 |
| 完全相關 | 不相關 | 高度相關 | 低度相關 | 中度相關 |
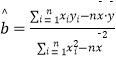 ,
, ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com