
分析 (1利用q=$\root{4}{\frac{{a}_{5}}{{a}_{1}}}$,即可得出.
(2)利用等比數列的求和公式可得f(n)=$\frac{4}{3}({4}^{n}-1)$,f(n+1)=$\frac{4}{3}({4}^{n+1}-1)$.再利用極限的運算法則即可得出.
(3)由a1b1+a2b2+…+anbn=(n-1)•2n+1+2,當n≥2時,a1b1+a2b2+…+an-1bn-1=(n-2)•2n+2,兩式相減得:可得bn=$\frac{n•{2}^{n}}{{2}^{n}}$=n(n≥2),b1=1滿足上式,可得bn=n.設Sn表示數列{cn}的前n項之和,S100=(a1+a2+…+a50)+(b1+b2+…+b50),即可得出.
解答 解:(1)∵a1=2,a5=32,
∴q=$\root{4}{\frac{{a}_{5}}{{a}_{1}}}$=2,
∴an=2n.
(2)f(n)=a2+a4+…+a2n=22+24+…+22n=$\frac{4({4}^{n}-1)}{4-1}$=$\frac{4}{3}({4}^{n}-1)$,f(n+1)=$\frac{4}{3}({4}^{n+1}-1)$.
∴$\underset{lim}{n→∞}\frac{f(n+1)}{f(n)}$=$\underset{lim}{n→∞}$$\frac{{4}^{n+1}-1}{{4}^{n}-1}$=$\underset{lim}{n→∞}\frac{4-\frac{1}{{4}^{n}}}{1-\frac{1}{{4}^{n}}}$=4.
(3)∵a1b1+a2b2+…+anbn=(n-1)•2n+1+2,
∴當n≥2時,a1b1+a2b2+…+an-1bn-1=(n-2)•2n+2,
兩式相減得:anbn=(n-1)•2n+1+2-(n-2)•2n+2=n•2n,即bn=$\frac{n•{2}^{n}}{{2}^{n}}$=n(n≥2),
又∵a1b1=2,即b1=1滿足上式,
∴bn=n;
設Sn表示數列{cn}的前n項之和,
S100=(a1+a2+…+a50)+(b1+b2+…+b50)
=2+22+…+250+1+2+…+50
=$\frac{2({2}^{50}-1)}{2-1}$+$\frac{50×51}{2}$
=251+1273.
點評 本題考查了等差數列與等比數列的通項公式與求和公式、遞推關系,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [5,e2) | B. | [5,7] | C. | {5,6,7} | D. | {5,6,7,8} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | k=-6 | B. | k=2 | C. | k=6 | D. | k=-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
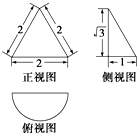
| A. | $\frac{3}{2}π$ | B. | $\frac{3}{2}π+\sqrt{3}$ | C. | $π+\sqrt{3}$ | D. | $\frac{5}{2}π+\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com