
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為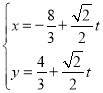 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在平面直角坐標系![]() 中,設直線
中,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.若點
兩點.若點![]() 恰為線段
恰為線段![]() 的三等分點,求
的三等分點,求![]() 的值.
的值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為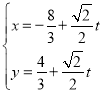 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在平面直角坐標系![]() 中,設直線
中,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.若點
兩點.若點![]() 恰為線段
恰為線段![]() 的三等分點,求
的三等分點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的首項a1=1,前n項和為Sn.設λ與k是常數,若對一切正整數n,均有
的首項a1=1,前n項和為Sn.設λ與k是常數,若對一切正整數n,均有![]() 成立,則稱此數列為“λ~k”數列.
成立,則稱此數列為“λ~k”數列.
(1)若等差數列![]() 是“λ~1”數列,求λ的值;
是“λ~1”數列,求λ的值;
(2)若數列![]() 是“
是“![]() ”數列,且an>0,求數列
”數列,且an>0,求數列![]() 的通項公式;
的通項公式;
(3)對于給定的λ,是否存在三個不同的數列![]() 為“λ~3”數列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由,
為“λ~3”數列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知圓![]() ,圓
,圓![]() ,動圓
,動圓![]() 與圓
與圓![]() 外切并且與圓
外切并且與圓![]() 內切,圓心
內切,圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是與圓
是與圓![]() ,圓
,圓![]() 都相切的一條直線,
都相切的一條直線,![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,當圓
兩點,當圓![]() 的半徑最長時,求
的半徑最長時,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
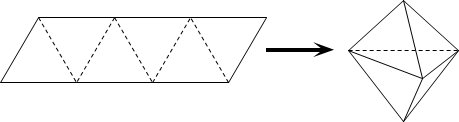
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽籺,俗稱“粽子”,古稱“角黍”,是端午節大家都會品嘗的食品,傳說這是為了紀念戰國時期楚國大臣、愛國主義詩人屈原.如圖,平行四邊形形狀的紙片是由六個邊長為1的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為____;若該六面體內有一球,則該球體積的最大值為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】洛書,古稱龜書,是陰陽五行術數之源,被世界公認為組合數學的鼻祖,它是中華民族對人類的偉大貢獻之一.在古代傳說中有神龜出于洛水,其甲殼上有圖1:“以五居中,五方白圈皆陽數,四隅黑點為陰數”,這就是最早的三階幻方,按照上述說法,將1到9這九個數字,填在如圖2所示的九宮格里,九宮格的中間填5,四個角填偶數,其余位置填奇數.則每一橫行、每一豎列以及兩條對角線上3個數字的和都等于15的概率是( )
圖1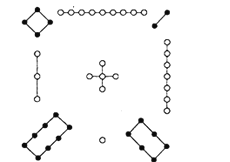 圖2
圖2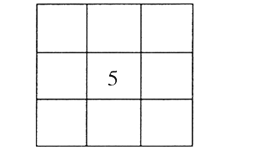
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應綠色出行,某市推出了新能源分時租賃汽車,并對該市市民使用新能源租賃汽車的態度進行調查,得到有關數據如下表1:
表1
愿意使用新能源租賃汽車 | 不愿意使用新能源租賃汽車 | 總計 | |
男性 | 100 | 300 | |
女性 | 400 | ||
總計 | 400 |
其中一款新能源分時租賃汽車的每次租車費用由行駛里程和用車時間兩部分構成:行駛里程按1元/公里計費;用車時間不超過30分鐘時,按0.15元/分鐘計費;超過30分鐘時,超出部分按0.20元/分鐘計費.已知張先生從家到上班地點15公里,每天上班租用該款汽車一次,每次的用車時間均在20~60分鐘之間,由于堵車紅綠燈等因素,每次的用車時間![]() (分鐘)是一個隨機變量.張先生記錄了100次的上班用車時間,并統計出在不同時間段內的頻數如下表2:
(分鐘)是一個隨機變量.張先生記錄了100次的上班用車時間,并統計出在不同時間段內的頻數如下表2:
表2
時間 | (20,30] | (30,40] | (40,50] | (50,60] |
頻數 | 20 | 40 | 30 | 10 |
(1)請補填表1中的空缺數據,并判斷是否有99.5%的把握認為該市市民對新能源租賃汽車的使用態度與性別有關;
(2)根據表2中的數據,將各時間段發生的頻率視為概率,以各時間段的區間中點值代表該時間段的取值,試估計張先生租用一次該款汽車上班的平均用車時間;
附: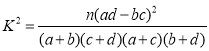
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com