
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為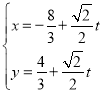 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在平面直角坐標系![]() 中,設直線
中,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.若點
兩點.若點![]() 恰為線段
恰為線段![]() 的三等分點,求
的三等分點,求![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】已知x與y之間的幾組數據如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表數據中y的平均值為2.5,若某同學對m賦了三個值分別為1.5,2,2.5,得到三條線性回歸直線方程分別為![]() ,
,![]() ,
,![]() ,對應的相關系數分別為
,對應的相關系數分別為![]() ,
,![]() ,
,![]() ,下列結論中錯誤的是( )
,下列結論中錯誤的是( )
參考公式:線性回歸方程![]() 中,其中
中,其中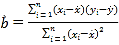 ,
,![]() .相關系數
.相關系數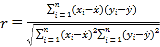 .
.
A.三條回歸直線有共同交點B.相關系數中,![]() 最大
最大
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區為了調查本小區業主對物業服務滿意度的真實情況,對本小區業主進行了調查,調查中問了兩個問題1:你的手機尾號是不是奇數?問題2:你是否滿意物業的服務?調查者設計了一個隨機化裝置,其中裝有大小、形狀和質量完全相同的白球和紅球,每個被調查者隨機從裝置中摸到紅球和白球的可能性相同,其中摸到白球的業主回答第一個問題,摸到紅球的業主回答第二個問題,回答“是”的人往一個盒子中放一個小石子,回答“否”的人什么都不要做由于問題的答案只有“是”和“否”,而且回答的是哪個問題別人并不知道,因此被調查者可以毫無顧慮地給出符合實際情況的答案.已知某小區80名業主參加了問卷,且有47名業主回答了“是”,由此估計本小區對物業服務滿意的百分比大約為( )
A.85%B.75%C.63.5%D.67.5%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,點
上,點![]() 在圓
在圓![]() 上,且圓
上,且圓![]() 上的所有點均在橢圓
上的所有點均在橢圓![]() 外,若
外,若![]() 的最小值為
的最小值為![]() ,且橢圓
,且橢圓![]() 的長軸長恰與圓
的長軸長恰與圓![]() 的直徑長相等,則下列說法正確的是( )
的直徑長相等,則下列說法正確的是( )
A.橢圓![]() 的焦距為
的焦距為![]() B.橢圓
B.橢圓![]() 的短軸長為
的短軸長為![]()
C.![]() 的最小值為
的最小值為![]() D.過點
D.過點![]() 的圓
的圓![]() 的切線斜率為
的切線斜率為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大提出:堅決打贏脫貧攻堅戰,做到精準扶貧.某縣積極引導農民種植一種名貴中藥材,從而大大提升了該縣村民的經濟收入.2019年年底,該機構從該縣種植的這種名貴藥材的農戶中隨機抽取了100戶,統計了他們2019年因種植,中藥材所獲純利潤(單位:萬元)的情況(假定農戶因種植中藥材這一項一年最多獲利11萬元),統計結果如下表所示:
![]()
(1)由表可以認為,該縣農戶種植中藥材所獲純利潤Z(單位:萬元)近似地服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() (每組數據取區間的中點值),
(每組數據取區間的中點值),![]() 近似為樣本方差
近似為樣本方差![]() .若該縣有1萬戶農戶種植了該中藥材,試估算所獲純利潤Z在區間(1.9,8.2)的戶數;
.若該縣有1萬戶農戶種植了該中藥材,試估算所獲純利潤Z在區間(1.9,8.2)的戶數;
(2)為答謝廣大農戶的積極參與,該調查機構針對參與調查的農戶舉行了抽獎活動,抽獎規則如下:在一箱子中放置5個除顏色外完全相同的小球,其中紅球1個,黑球4個.讓農戶從箱子中隨機取出一個小球,若取到紅球,則抽獎結束;若取到黑球,則將黑球放回箱中,讓他繼續取球,直到取到紅球為止(取球次數不超過10次).若農戶取到紅球,則視為中獎,獲得2000元的獎勵,若一直未取到紅球,則視為不中獎.現農戶張明參加了抽獎活動,記他中獎時取球的次數為隨機變量X,他取球的次數為隨機變量Y.
①證明:![]() 為等比數列;
為等比數列;
②求Y的數學期望.(精確到0.001)
參考數據:![]() .若隨機變量
.若隨機變量![]() 則
則![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著2022年北京冬奧會的臨近,中國冰雪產業快速發展,冰雪運動人數快速上升,冰雪運動市場需求得到釋放.如圖是2012-2018年中國雪場滑雪人數(單位:萬人)與同比增長情況統計圖則下面結論中正確的是( ).
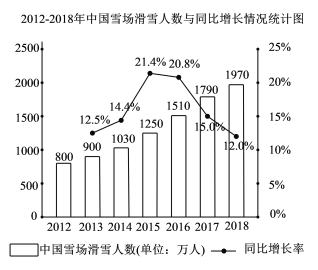
A.2012-2018年,中國雪場滑雪人數逐年增加;
B.2013-2015年,中國雪場滑雪人數和同比增長率均逐年增加;
C.中國雪場2015年比2014年增加的滑雪人數和2018年比2017年增加的滑雪人數均為220萬人,因此這兩年的同比增長率均有提高;
D.2016-2018年,中國雪場滑雪人數的增長率約為23.4%.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春節突如其來的新型冠狀病毒肺炎在湖北爆發,一方有難八方支援,全國各地的白衣天使走上戰場的第一線,某醫院抽調甲、乙兩名醫生,抽調![]() 、
、![]() 、
、![]() 三名護士支援武漢第一醫院與第二醫院,參加武漢疫情狙擊戰其中選一名護士與一名醫生去第一醫院,其它都在第二醫院工作,則醫生甲和護士
三名護士支援武漢第一醫院與第二醫院,參加武漢疫情狙擊戰其中選一名護士與一名醫生去第一醫院,其它都在第二醫院工作,則醫生甲和護士![]() 被選在第一醫院工作的概率為( )
被選在第一醫院工作的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為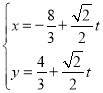 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在平面直角坐標系![]() 中,設直線
中,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.若點
兩點.若點![]() 恰為線段
恰為線段![]() 的三等分點,求
的三等分點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
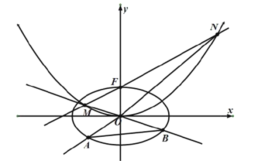
【題目】如圖,已知橢圓![]() ,點
,點![]() 是拋物線
是拋物線![]() 的焦點,過點F作直線
的焦點,過點F作直線![]() 交拋物線于M,N兩點,延長
交拋物線于M,N兩點,延長![]() ,
,![]() 分別交橢圓于A,B兩點,記
分別交橢圓于A,B兩點,記![]() ,
,![]() 的面積分別是
的面積分別是![]() ,
,![]() .
.
(1)求![]() 的值及拋物線的準線方程;
的值及拋物線的準線方程;
(2)求![]() 的最小值及此時直線
的最小值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com