
如圖,四邊形ABCD內接于圓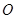 ,BD是圓
,BD是圓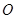 的直徑,
的直徑,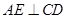 于點E,DA平分
于點E,DA平分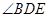 .
.
(1)證明:AE是圓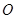 的切線;
的切線;
(2)如果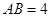 ,
,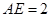 ,求CD.
,求CD.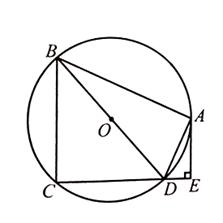
(1)證明過程詳見解析;(2)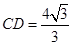 .
.
解析試題分析:本題主要考查三角形相似、內錯角相等、弦切角相等、切割線定理等基礎知識,考查學生的邏輯推理能力、轉化能力.第一問,連結OA,利用OA,OD都是半徑,得∠OAD=∠ODA,利用傳遞性∠ODA=∠ADE,得∠ADE=∠OAD,利用內錯角相等,得OA∥CE,所以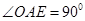 ,所以AE為圓O的切線;第二問,利用第一問的分析得△ADE∽△BDA,所以
,所以AE為圓O的切線;第二問,利用第一問的分析得△ADE∽△BDA,所以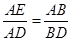 ,即BD=2AD,所以在
,即BD=2AD,所以在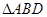 中,得
中,得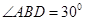 ,利用弦切角相等得
,利用弦切角相等得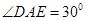 ,在
,在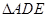 中,求出DE的長,再利用切割線定理得CD的長.
中,求出DE的長,再利用切割線定理得CD的長.
(1)連結OA,則OA=OD,所以∠OAD=∠ODA,
又∠ODA=∠ADE,所以∠ADE=∠OAD,所以OA∥CE.
因為AE⊥CE,所以OA⊥AE.
所以AE是⊙O的切線. 5分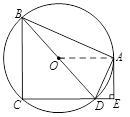
(2)由(1)可得△ADE∽△BDA,
所以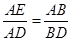 ,即
,即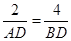 ,則BD=2AD,
,則BD=2AD,
所以∠ABD=30°,從而∠DAE=30°,
所以DE=AEtan30°=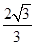 .
.
由切割線定理,得AE2=ED·EC,
所以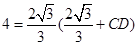 ,所以
,所以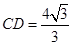 . 10分
. 10分
考點:三角形相似、內錯角相等、弦切角相等、切割線定理.


科目:高中數學 來源: 題型:解答題
扇形AOB中心角為60°,所在圓半徑為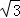 ,它按如下(Ⅰ)(Ⅱ)兩種方式有內接矩形CDEF.
,它按如下(Ⅰ)(Ⅱ)兩種方式有內接矩形CDEF.
(Ⅰ)矩形CDEF的頂點C、D在扇形的半徑OB上,頂點E在圓弧AB上,頂點F在半徑OA上,設∠EOB=θ;
(Ⅱ)點M是圓弧AB的中點,矩形CDEF的頂點D、E在圓弧AB上,且關于直線OM對稱,頂點C、F分別在半徑OB、OA上,設∠EOM= ;
;
試研究(Ⅰ)(Ⅱ)兩種方式下矩形面積的最大值,并說明兩種方式下哪一種矩形面積最大?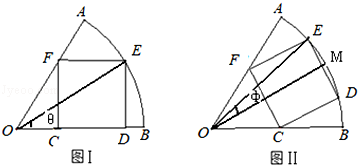
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有一塊直角三角形木板,如圖所示,∠C=90°,AB=5 cm,BC=3 cm,AC=4 cm,根據需要,要把它加工成一個面積最大的正方形木板,設計一個方案,應怎樣裁才能使正方形木板面積最大,并求出這個正方形木板的邊長.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,圓O是等腰三角形ABC的外接圓,AB=AC,延長BC到點D,使CD=AC,連結AD交圓O于點E,連結BE與AC交于點F.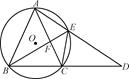
(1)判斷BE是否平分∠ABC,并說明理由;
(2)若AE=6,BE=8,求EF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com