
已知數列![]() 的首項
的首項![]() 前
前![]() 項和為
項和為![]() ,且
,且![]()
(I)證明數列![]() 是等比數列;
是等比數列;
(II)令![]() ,求函數
,求函數![]() 在點
在點![]() 處的導數
處的導數![]() 并比較
并比較![]() 與
與![]() 的大小.
的大小.
解:(Ⅰ)由已知![]()
∴![]() 時,
時,![]()
兩式相減,得![]() ,
,
即![]() ,從而
,從而![]() ,
,
當![]() 時
時![]()
∴![]()
又![]() ,∴
,∴![]() ,從而
,從而 ![]()
故總有![]() 、
、
又∵![]() ∴
∴![]() 從而
從而![]()
即![]() 是以
是以![]() 為首項,2為公比的等比數列。
為首項,2為公比的等比數列。
(II)由(I)知![]() 。
。
∵![]()
∴![]() 。
。
從而 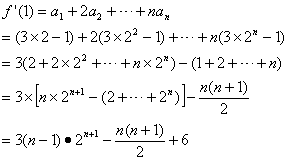
由上 ![]()
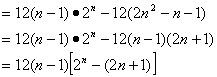 (*)
(*)
當![]() 時,(*)式=0 ∴
時,(*)式=0 ∴![]() ;
;
當![]() 時,(*)式=-12
時,(*)式=-12![]() ∴
∴![]()
當![]() 時,
時, ![]()
又![]()
∴![]()
即(*)![]()
從而![]()
(或用數學歸納法:n≥3時,猜想 ![]()
由于n-1>0,只要證明2n>2n+1。事實上,
1* 當 n=3時,23>2×3+1
不等式成立,
2* 設n=k時(k≥3),有2k>2k+1
則 2k+1>2(2k+1)
=4k+2
=2(k+1)+1+(2k-1).
∵k≥3,∴2k-1>0.
從而 2k+1>2(k+1)+1+(2k-1)
>2(k+1)+1
即 n=k+1時,亦有 2n>2n+1.
綜上1*、2*知,2n>2n+1 對n≥3,n∈N* 都成立。
∴n≥3時,有![]()
綜上 n=1時,![]()
n=2時,![]()
n≥3時,![]()


科目:高中數學 來源:2015屆浙江省寧波市高一下學期期中考試文科數學試卷(解析版) 題型:解答題
已知數列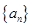 的首項
的首項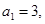 前
前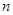 項和為
項和為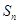 ,且
,且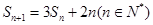 ,
,
(1)試判斷數列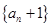 是否成等比數列?并求出數列
是否成等比數列?并求出數列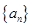 的通項公式;
的通項公式;
(2)記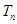 為數列
為數列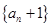 前
前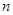 項和,求
項和,求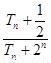 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com