

分析 (1)取PD的中點N,連接AN,MN,由三角形中位線定理可得及已知可得四邊形ABMN為平行四邊形,得AN∥BM,在由已知BM⊥平面PCD,可得AN⊥平面PCD,由面面垂直的判定可得平面PAD⊥平面PCD;
(2)取AD的中點O,連接PO,由AN⊥平面PCD,可得AN⊥PD,AN⊥CD.再由已知可得△PAD為等邊三角形,得到CD⊥AD,則平面PAD⊥平面ABCD.再由線面垂直的性質可得PO是錐P-ABCD的高.由已知直線PC與AB所成角的正切值為$\frac{1}{2}$,AB=1求得CD=2,PA=AD=AB=1,再由棱錐體積公式求得四棱錐P-ABCD的體積.
解答 (1)證明:取PD的中點N,連接AN,MN,則$MN∥CD,MN=\frac{1}{2}CD$,
又$AB∥CD,AB=\frac{1}{2}CD$,∴MN∥AB,MN=AB,
則四邊形ABMN為平行四邊形,∴AN∥BM,
又BM⊥平面PCD,∴AN⊥平面PCD,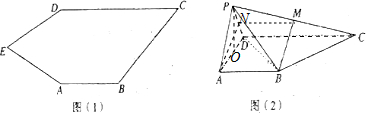
∵AN⊆面PCD,
∴平面PAD⊥平面PCD;
(2)解:取AD的中點O,連接PO,
∵AN⊥平面PCD,
∴AN⊥PD,AN⊥CD.
由ED=EA,即PD=PA及N為PD的中點,可得△PAD為等邊三角形,
∴∠PDA=60°,
又∠EDC=150°,∴∠CDA=90°,則CD⊥AD,
∴CD⊥平面PAD,CD?平面ABCD,
∴平面PAD⊥平面ABCD.
∵PO⊥AD,面PAD∩面ABCD=AD,PO?面PAD,
∴PO⊥面ABCD,
PO是錐P-ABCD的高.
∵AB∥CD,∴∠PCD為直線PC與AB所成的角,
由(1)可得∠PDC=90°,∴$tan∠PCD=\frac{PD}{CD}=\frac{1}{2}$,得CD=2PD,
由AB=1,可知CD=2,PA=AD=AB=1,
∴PO=$\sqrt{1-(\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$,
${S}_{ABCD}=\frac{1}{2}(1+2)×2=3$.
則${V}_{P-ABCD}=\frac{1}{3}•{S}_{ABCD}•PO$=$\frac{1}{3}×3×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
點評 本題考查平面與平面垂直的判定,考查空間想象能力和思維能力,訓練了多面體體積的求法,是中檔題.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.E是AP的中點.
如圖,在四棱錐P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.E是AP的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6π | B. | 36π | C. | 7π | D. | 49π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2016 | B. | 1008 | C. | 504 | D. | 2017 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
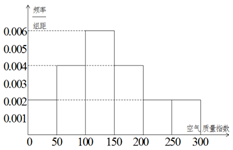 某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如表(假設該區域空氣質量指數不會超過300):
某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如表(假設該區域空氣質量指數不會超過300):| 空氣質量指數 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空氣質量等級 | 1級優 | 2級良 | 3級輕度 污染 | 4級中度 污染 | 5級重度 污染 | 6級嚴重污染 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{7}{32}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com