
分析 (1)一臺機器運行是否出現(xiàn)故障看作一次實驗,在一次試驗中,機器出現(xiàn)故障的概率為$\frac{1}{3}$;
4臺機器相當于4次獨立重復(fù)試驗,設(shè)出現(xiàn)故障的機器臺數(shù)為X,$X~B({4,\frac{1}{3}})$,求出對應(yīng)概率值,
寫出分布列,計算“每臺機器在任何時刻同時出現(xiàn)故障時能及時進行維修”的概率不少于90%的對應(yīng)工人數(shù);
(2)設(shè)該廠獲利為Y萬元,Y的所有可能取值為18,13,8,計算對應(yīng)的概率值,求出分布列與數(shù)學(xué)期望值.
解答 解:(1)一臺機器運行是否出現(xiàn)故障可看作一次實驗,
在一次試驗中,機器出現(xiàn)故障設(shè)為事件A,則事件A的概率為$\frac{1}{3}$;
該廠有4臺機器就相當于4次獨立重復(fù)試驗,
可設(shè)出現(xiàn)故障的機器臺數(shù)為X,則$X~B({4,\frac{1}{3}})$,
$P({X=0})=C_4^0{({\frac{2}{3}})^4}=\frac{16}{81}$,
$P({X=1})=C_4^1•\frac{1}{3}•{({\frac{2}{3}})^3}=\frac{32}{81}$,
$P({X=2})=C_4^2•{({\frac{1}{3}})^2}{({\frac{2}{3}})^2}=\frac{24}{81}$,
$P({X=3})=C_4^3•{({\frac{1}{3}})^3}•\frac{2}{3}=\frac{8}{81}$,
則X的分布列為:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{16}{81}$ | $\frac{32}{81}$ | $\frac{24}{81}$ | $\frac{8}{81}$ | $\frac{1}{81}$ |
| n | 0 | 1 | 2 | 3 | 4 |
| P(X≤n) | $\frac{16}{81}$ | $\frac{48}{81}$ | $\frac{72}{81}$ | $\frac{80}{81}$ | 1 |
| Y | 18 | 13 | 8 |
| P | $\frac{72}{81}$ | $\frac{8}{81}$ | $\frac{1}{81}$ |
點評 本題考查了離散型隨機變量的分布列與數(shù)學(xué)期望的計算問題,是綜合性題目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | ?x0<0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C. | ?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$ | D. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
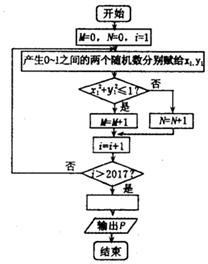 如圖所示,使用模擬方法估計圓周率值的程序框閏,P表示估計的結(jié)果,剛圖中空白框內(nèi)應(yīng)填入P=( )
如圖所示,使用模擬方法估計圓周率值的程序框閏,P表示估計的結(jié)果,剛圖中空白框內(nèi)應(yīng)填入P=( )| A. | $\frac{M}{2017}$ | B. | $\frac{2017}{M}$ | C. | $\frac{4M}{2017}$ | D. | $\frac{2017}{4M}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (-2,+∞) | B. | (-2,2) | C. | (-∞,-2) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 20% 369 | B. | 80% 369 | C. | 40% 360 | D. | 60% 365 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com