
分析 根據導數的概念得出 $\frac{f(x)-f(0)}{x}$>k>1,用x=$\frac{1}{k-1}$代入可判斷出f($\frac{1}{k-1}$)>$\frac{1}{k-1}$,即可判斷答案.
解答 解;∵f′(x)=$\underset{lim}{x→0}$$\frac{f(x)-f(0)}{x-0}$,f′(x)>k>1,
∴$\frac{f(x)-f(0)}{x}$>k>1,
即 $\frac{f(x)+1}{x}$>k>1,
x=$\frac{1}{k}$時,f($\frac{1}{k}$)+1>$\frac{1}{k}$•k=1>0,故①正確,②錯誤;
當x=$\frac{1}{k-1}$時,f($\frac{1}{k-1}$)+1>$\frac{1}{k-1}$×k=$\frac{k}{k-1}$,
即f($\frac{1}{k-1}$)>$\frac{k}{k-1}$-1=$\frac{1}{k-1}$,
故f($\frac{1}{k-1}$)>$\frac{1}{k-1}$,故③正確,④錯誤;
故選:①③.
點評 本題考查了導數的概念,不等式的化簡運算,屬于中檔題,理解了變量的代換問題.


科目:高中數學 來源: 題型:解答題
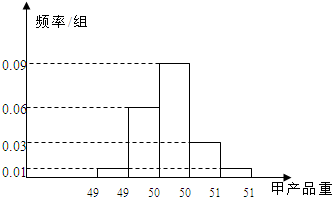 某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況,隨機在這兩條流水線上各抽取40件產品作為樣本.經統計,得到關于產品重量的樣本頻率分布直方圖和樣本頻數分布表:
某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況,隨機在這兩條流水線上各抽取40件產品作為樣本.經統計,得到關于產品重量的樣本頻率分布直方圖和樣本頻數分布表:| 乙流水線 產品重量(單位:克) | 頻數 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,將菱形ABCD沿對角線BD折起,使得C點至C′,E點 在線段AC′上,若二面角A-BD-E與二面角E-BD-C′的大小分別為和45°和30°,則$\frac{AE}{EC′}$=( )
如圖,將菱形ABCD沿對角線BD折起,使得C點至C′,E點 在線段AC′上,若二面角A-BD-E與二面角E-BD-C′的大小分別為和45°和30°,則$\frac{AE}{EC′}$=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com