
【題目】設數列![]() 共有
共有![]() 項,記該數列前
項,記該數列前![]() 項
項![]() ,
,![]() ,…,
,…,![]() 中的最大項為
中的最大項為![]() ,該數列后
,該數列后![]() 項
項![]() ,
,![]() ,…,
,…,![]() 中的最小項為
中的最小項為![]() ,
,![]() (
(![]() 1,2,3,…,
1,2,3,…,![]() ).
).
(1)若數列![]() 的通項公式為
的通項公式為![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 是單調數列,且滿足
是單調數列,且滿足![]() ,
,![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3)試構造一個數列![]() ,滿足
,滿足![]() ,其中
,其中![]() 是公差不為零的等差數列,
是公差不為零的等差數列,![]() 是等比數列,使得對于任意給定的正整數
是等比數列,使得對于任意給定的正整數![]() ,數列
,數列![]() 都是單調遞增的,并說明理由.
都是單調遞增的,并說明理由.
科目:高中數學 來源: 題型:
【題目】談祥柏先生是我國著名的數學科普作家,他寫的《數學百草園》、《好玩的數學》、《故事中的數學》等書,題材廣泛、妙趣橫生,深受廣大讀者喜愛.下面我們一起來看《好玩的數學》中談老的一篇文章《五分鐘內挑出埃及分數》:文章首先告訴我們,古埃及人喜歡使用分子為1的分數(稱為埃及分數).如用兩個埃及分數![]() 與
與![]() 的和表示
的和表示![]() 等.從
等.從![]() 這100個埃及分數中挑出不同的3個,使得它們的和為1,這三個分數是________.(按照從大到小的順序排列)
這100個埃及分數中挑出不同的3個,使得它們的和為1,這三個分數是________.(按照從大到小的順序排列)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
已知數列![]() 和
和![]() 滿足:
滿足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 為實數,
為實數,![]() 為正整數.
為正整數.
(Ⅰ)對任意實數![]() ,證明:數列
,證明:數列![]() 不是等比數列;
不是等比數列;
(Ⅱ)證明:當![]() 時,數列
時,數列![]() 是等比數列;
是等比數列;
(Ⅲ)設![]() (
(![]() 為實常數),
為實常數),![]() 為數列
為數列![]() 的前
的前![]() 項和.是否存在實數
項和.是否存在實數![]() ,使得對任意正整數
,使得對任意正整數![]() ,都有
,都有![]() ?若存在,求
?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:在直角坐標系![]() 中,設橢圓
中,設橢圓![]() 的左右兩個焦點分別為
的左右兩個焦點分別為![]() 、
、![]() .過右焦點
.過右焦點![]() 與
與![]() 軸垂直的直線
軸垂直的直線![]() 與橢圓C相交,其中一個交點為
與橢圓C相交,其中一個交點為![]() .
.
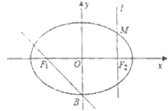
(1)求橢圓C的方程;
(2)設橢圓C的一個頂點為![]() ,求點M到直線
,求點M到直線![]() 的距離;
的距離;
(3)過![]() 中點的直線
中點的直線![]() 交橢圓于P、Q兩點,求
交橢圓于P、Q兩點,求![]() 長的最大值以及相應的直線方程.
長的最大值以及相應的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如題所示:扇形ABC是一塊半徑為2千米,圓心角為60°的風景區,P點在弧BC上,現欲在風景區中規劃三條三條商業街道PQ、QR、RP,要求街道PQ與AB垂直,街道PR與AC垂直,直線PQ表示第三條街道。
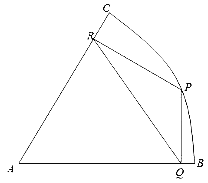
(1)如果P位于弧BC的中點,求三條街道的總長度;
(2)由于環境的原因,三條街道PQ、PR、QR每年能產生的經濟效益分別為每千米300萬元、200萬元及400萬元,問:這三條街道每年能產生的經濟總效益最高為多少?(精確到1萬元)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過點
,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 兩點,延長
兩點,延長![]() 交橢圓
交橢圓![]() 于點
于點![]() ,
,![]() 的周長為8.
的周長為8.

(1)求![]() 的離心率及方程;
的離心率及方程;
(2)試問:是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于x的方程2x2﹣ax﹣2=0的兩根分別為α、β(α<β),函數![]()
(1)證明f(x)在區間(α,β)上是增函數;
(2)當a為何值時,f(x)在區間[α,β]上的最大值與最小值之差最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() :
:![]() 的焦點,直線
的焦點,直線![]() 與拋物線
與拋物線![]() 相切于點
相切于點![]() ,連接
,連接![]() 交拋物線于另一點
交拋物線于另一點![]() ,過點
,過點![]() 作
作![]() 的垂線交拋物線
的垂線交拋物線![]() 于另一點
于另一點![]() .
.
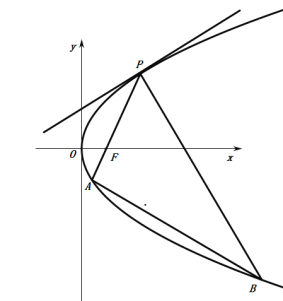
(1)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)求三角形![]() 面積
面積![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com