
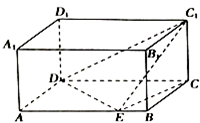
 如圖,在長方體ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是線段AB上的點,且EB=1,則二面角C-DE-C1的正切值為$\frac{\sqrt{2}}{2}$.
如圖,在長方體ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是線段AB上的點,且EB=1,則二面角C-DE-C1的正切值為$\frac{\sqrt{2}}{2}$. 分析 過點C作CF⊥DE于F,連結C1F,說明∠C1FC就是二面角C-DE-C1的平面角,在△C1FC中,∠C1CF=90°,求解tan∠C1FC的值即可.
解答 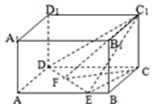 解:過點C作CF⊥DE于F,連結C1F,因為DE⊥C1C,所以DE⊥平面C1CF,所以C1F⊥DE,
解:過點C作CF⊥DE于F,連結C1F,因為DE⊥C1C,所以DE⊥平面C1CF,所以C1F⊥DE,
所以∠C1FC就是二面角C-DE-C1的平面角,
在△C1FC中,∠C1CF=90°,CF=CDsin45$°=2\sqrt{2}$.
所以tan∠C1FC=$\frac{C{C}_{1}}{CF}$=$\frac{\sqrt{2}}{2}$.
故答案為:$\frac{\sqrt{2}}{2}$.
點評 本題考查二面角的平面角的求法,考查空間想象能力以及計算能力,轉化思想的應用.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
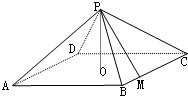 如圖:四棱錐P-ABCD中,底面是以O為中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的點,且BM=$\frac{1}{2}$,
如圖:四棱錐P-ABCD中,底面是以O為中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的點,且BM=$\frac{1}{2}$,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
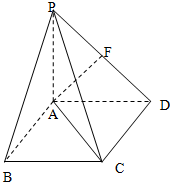 如圖,四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是邊長為2的正方形,PA=AD,F為PD的中點.
如圖,四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是邊長為2的正方形,PA=AD,F為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
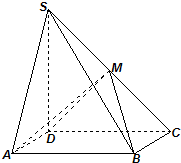 如圖,四棱錐S-ABCD中,底面ABCD為矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,點M是側棱SC的中點.
如圖,四棱錐S-ABCD中,底面ABCD為矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,點M是側棱SC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com