
【題目】已知橢圓E: ![]() (a﹥b﹥0)的一個焦點與短軸的兩個端點是正三角形的三個頂點,點
(a﹥b﹥0)的一個焦點與短軸的兩個端點是正三角形的三個頂點,點![]() 在橢圓E上.
在橢圓E上.
(Ⅰ)求橢圓E的方程;
(Ⅱ)設不過原點O且斜率為![]() 的直線l與橢圓E交于不同的兩點A,B,線段AB的中點為M,直線OM與橢圓E交于C,D,證明:|MA|·|MB|=|MC|·|MD|.
的直線l與橢圓E交于不同的兩點A,B,線段AB的中點為M,直線OM與橢圓E交于C,D,證明:|MA|·|MB|=|MC|·|MD|.
 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線![]()
![]() 的焦點為
的焦點為![]() ,過拋物線
,過拋物線![]() 上的動點
上的動點![]() (除頂點
(除頂點![]() 外)作
外)作![]() 的切線
的切線![]() 交
交![]() 軸于點
軸于點![]() .過點
.過點![]() 作直線
作直線![]() 的垂線
的垂線![]() (垂足為
(垂足為![]() )與直線
)與直線![]() 交于點
交于點![]() .
.
(Ⅰ)求焦點![]() 的坐標;
的坐標;
(Ⅱ)求證:![]() ;
;
(Ⅲ)求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的首項為
的首項為![]() ,公差為
,公差為![]() ,等比數列
,等比數列![]() 的首項為
的首項為![]() ,公比為
,公比為![]() .
.
(Ⅰ)若數列![]() 的前
的前![]() 項和
項和![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若![]() ,
, ![]() ,且
,且![]() .
.
(i)求![]() 的值;
的值;
(ii)對于數列![]() 和
和![]() ,滿足關系式
,滿足關系式![]() ,
, ![]() 為常數,且
為常數,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的導函數f′(x),且對任意x>0,都有f′(x)>![]() .
.
(1)判斷函數F(x)=![]() 在(0,+∞)上的單調性;
在(0,+∞)上的單調性;
(2)設x1,x2∈(0,+∞),證明:f(x1)+f(x2)<f(x1+x2);
(3)請將(2)中結論推廣到一般形式,并證明你所推廣的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,射線OA、OB分別與x軸正半軸成45°和30°角,過點P(1,0)作直線AB分別交OA、OB于A、B兩點,當AB的中點C恰好落在直線y=![]() x上時,求直線AB的方程.
x上時,求直線AB的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2-ax-xln x,且f(x)≥0.
(1)求a;
(2)證明:f(x)存在唯一的極大值點x0,且e-2<f(x0)<2-2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是由
是由![]() 個實數組成的
個實數組成的![]() 行
行![]() 列的數表,滿足:每個數的絕對值不大于
列的數表,滿足:每個數的絕對值不大于![]() ,且所有數的和為零,記
,且所有數的和為零,記![]() 為所有這樣的數表組成的集合,對于
為所有這樣的數表組成的集合,對于![]() ,記
,記![]() 為
為![]() 的第
的第![]() 行各數之和(
行各數之和(![]() 剟
剟![]()
![]() ),
),![]() 為
為![]() 的第
的第![]() 列各數之和(
列各數之和(![]() 剟
剟![]() ),記
),記![]() 為
為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 中的最小值.
中的最小值.
(![]() )對如下數表
)對如下數表![]() ,求
,求![]() 的值.
的值.
|
|
|
|
|
|
(![]() )設數表
)設數表![]() 形如:
形如:
|
|
|
|
|
|
求![]() 的最大值.
的最大值.
(![]() )給定正整數
)給定正整數![]() ,對于所有的
,對于所有的![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·鄭州第二次質量預測)如圖,高為1的等腰梯形ABCD中,AM=CD=![]() AB=1.現將△AMD沿MD折起,使平面AMD⊥平面MBCD,連接AB,AC.
AB=1.現將△AMD沿MD折起,使平面AMD⊥平面MBCD,連接AB,AC.
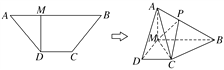
(1)在AB邊上是否存在點P,使AD∥平面MPC?
(2)當點P為AB邊的中點時,求點B到平面MPC的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com