
【題目】已知函數f(x)=ax2-ax-xln x,且f(x)≥0.
(1)求a;
(2)證明:f(x)存在唯一的極大值點x0,且e-2<f(x0)<2-2.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:![]() 通過分析可知
通過分析可知![]() 等價于
等價于![]() ,進而利用
,進而利用![]() 可得
可得![]() ,從而可得結論;
,從而可得結論;
![]() 通過
通過![]() 可知
可知![]() ,記
,記![]() ,解不等式可知
,解不等式可知![]() ,從而可知
,從而可知![]() 存在兩根
存在兩根![]() ,利用
,利用![]() 必存在唯一極大值點
必存在唯一極大值點![]() 及
及![]() 可知
可知![]() ,另一方面可知
,另一方面可知![]()
解析:(1)解:因為f(x)=ax2﹣ax﹣xlnx=x(ax﹣a﹣lnx)(x>0),
則f(x)≥0等價于h(x)=ax﹣a﹣lnx≥0,求導可知h′(x)=a﹣![]() .
.
則當a≤0時h′(x)<0,即y=h(x)在(0,+∞)上單調遞減,
所以當x0>1時,h(x0)<h(1)=0,矛盾,故a>0.
因為當0<x<![]() 時h′(x)<0、當x>
時h′(x)<0、當x>![]() 時h′(x)>0,所以h(x)min=h(
時h′(x)>0,所以h(x)min=h(![]() ),
),
又因為h(1)=a﹣a﹣ln1=0,所以![]() =1,解得a=1;
=1,解得a=1;
(2)證明:由(1)可知f(x)=x2﹣x﹣xlnx,f′(x)=2x﹣2﹣lnx,
令f′(x)=0,可得2x﹣2﹣lnx=0,記t(x)=2x﹣2﹣lnx,則t′(x)=2﹣![]() ,
,
令t′(x)=0,解得:x=![]() ,
,
所以t(x)在區間(0,![]() )上單調遞減,在(
)上單調遞減,在(![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
所以t(x)min=t(![]() )=ln2﹣1<0,從而t(x)=0有解,即f′(x)=0存在兩根x0,x2,
)=ln2﹣1<0,從而t(x)=0有解,即f′(x)=0存在兩根x0,x2,
且不妨設f′(x)在(0,x0)上為正、在(x0,x2)上為負、在(x2,+∞)上為正,
所以f(x)必存在唯一極大值點x0,且2x0﹣2﹣lnx0=0,
所以f(x0)=![]() ﹣x0﹣x0lnx0=
﹣x0﹣x0lnx0=![]() ﹣x0+2x0﹣2
﹣x0+2x0﹣2![]() =x0﹣
=x0﹣![]() ,
,
由x0<![]() 可知f(x0)<(x0﹣
可知f(x0)<(x0﹣![]() )max=﹣
)max=﹣![]() +
+![]() =
=![]() ;
;
由f′(![]() )<0可知x0<
)<0可知x0<![]() <
<![]() ,
,
所以f(x)在(0,x0)上單調遞增,在(x0,![]() )上單調遞減,
)上單調遞減,
所以f(x0)>f(![]() )=
)=![]() ;
;
綜上所述,f(x)存在唯一的極大值點x0,且e﹣2<f(x0)<2﹣2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某公司為了準確把握市場,做好產品計劃,特對某產品做了市場調查:先銷售該產品50天,統計發現每天的銷售量![]() 分布在
分布在![]() 內,且銷售量
內,且銷售量![]() 的分布頻率
的分布頻率
 .
.
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若銷售量大于等于80,則稱該日暢銷,其余為滯銷,根據是否暢銷從這50天中用分層抽樣的方法隨機抽取5天,再從這5天中隨機抽取2天,求這2天中恰有1天是暢銷日的概率(將頻率視為概率).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知兩個正方形ABCD和DCEF不在同一平面內,M,N分別為AB,DF的中點.
(1)若平面ABCD⊥平面DCEF,求直線MN與平面DCEF所成角的正弦值;
(2)用反證法證明:直線ME與BN是兩條異面直線.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() (a﹥b﹥0)的一個焦點與短軸的兩個端點是正三角形的三個頂點,點
(a﹥b﹥0)的一個焦點與短軸的兩個端點是正三角形的三個頂點,點![]() 在橢圓E上.
在橢圓E上.
(Ⅰ)求橢圓E的方程;
(Ⅱ)設不過原點O且斜率為![]() 的直線l與橢圓E交于不同的兩點A,B,線段AB的中點為M,直線OM與橢圓E交于C,D,證明:|MA|·|MB|=|MC|·|MD|.
的直線l與橢圓E交于不同的兩點A,B,線段AB的中點為M,直線OM與橢圓E交于C,D,證明:|MA|·|MB|=|MC|·|MD|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·石家莊一模)祖暅是南北朝時期的偉大數學家,5世紀末提出體積計算原理,即祖暅原理:“冪勢既同,則積不容異”.意思是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平面的任何一個平面所截,如果截面面積都相等,那么這兩個幾何體的體積一定相等.現有以下四個幾何體:圖①是從圓柱中挖去一個圓錐所得的幾何體,圖②、圖③、圖④分別是圓錐、圓臺和半球,則滿足祖暅原理的兩個幾何體為( )
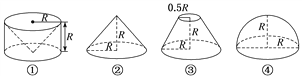
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市教育局對該市普通高中學生進行學業水平測試,試卷滿分120分,現從全市學生中隨機抽查了10名學生的成績,其莖葉圖如下圖所示:

(1)已知10名學生的平均成績為88,計算其中位數和方差;
(2)已知全市學生學習成績分布服從正態分布![]() ,某校實驗班學生30人.
,某校實驗班學生30人.
①依據(1)的結果,試估計該班學業水平測試成績在![]() 的學生人數(結果四舍五入取整數);
的學生人數(結果四舍五入取整數);
②為參加學校舉行的數學知識競賽,該班決定推薦成績在![]() 的學生參加預選賽若每個學生通過預選賽的概率為
的學生參加預選賽若每個學生通過預選賽的概率為![]() ,用隨機變量
,用隨機變量![]() 表示通過預選賽的人數,求
表示通過預選賽的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
正態分布參考數據: ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com