
設(shè)橢圓M:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,點A(a,0),B(0,-b)原點O到直線AB的距離為
,點A(a,0),B(0,-b)原點O到直線AB的距離為![]()
(Ⅰ)求橢圓M的方程;
(Ⅱ)設(shè)點C為(-a,0),點P在橢圓M上(與A、C均不重合),點E在直線PC上,若直線PA的方程為y=kx-4,且![]() ·
·![]() =0,試求直線BE的方程.
=0,試求直線BE的方程.
|
解:(Ⅰ)由 由點A(a,0),B(0,-b)知直線AB的方程為 于是可得直線AB的方程為x- 因此 所以橢圓m的方程為 (Ⅱ)由(Ⅰ)知A、B的坐標(biāo)依次為(2,0)、(0,- 因為直線PA經(jīng)過點A(2,0),所以0=2k-4,得k=2, 即得直線PA的方程為y=2x-4 因為 設(shè)P的坐標(biāo)為(x0,y0), (法Ⅰ)由 所以KBE=4 又點B的坐標(biāo)為(0,- (法Ⅱ)由橢圓的性質(zhì) 又 得- 又點B的坐標(biāo)為(0,- |


科目:高中數(shù)學(xué) 來源: 題型:
(09年豐臺區(qū)期末文)(14分)
設(shè)橢圓M:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,長軸長為
,長軸長為![]() ,設(shè)過右焦點F。
,設(shè)過右焦點F。
(Ⅰ)求橢圓M的方程;
(Ⅱ)設(shè)過右焦點F傾斜角為查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
設(shè)橢圓M:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,長軸長為
,長軸長為![]() ,設(shè)過右焦點F傾斜角為
,設(shè)過右焦點F傾斜角為![]() 的直線交橢圓M于A,B兩點。
的直線交橢圓M于A,B兩點。
(Ⅰ)求橢圓M的方程;
(Ⅱ)求證| AB | =![]() ;
;
(Ⅲ)設(shè)過右焦點F且與直線AB垂直的直線交橢圓M于C,D,求|AB| + |CD|的最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年山東省濟南市高三4月模擬考試文科數(shù)學(xué)卷 題型:解答題
設(shè)橢圓M: (a>b>0)的離心率與雙曲線
(a>b>0)的離心率與雙曲線
 的離心率互為倒數(shù),且內(nèi)切于圓
的離心率互為倒數(shù),且內(nèi)切于圓 .
.
(1)求橢圓M的方程;
(2)若直線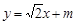 交橢圓于A、B兩點,橢圓上一點
交橢圓于A、B兩點,橢圓上一點 ,
,
求△PAB面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010河北省高三押題考試數(shù)學(xué)卷 題型:解答題
設(shè)橢圓M: (a>b>0)的離心率為
(a>b>0)的離心率為 ,長軸長為
,長軸長為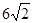 ,設(shè)過右焦點F傾斜角為
,設(shè)過右焦點F傾斜角為 的直線交橢圓M于A,B兩點。
的直線交橢圓M于A,B兩點。
(Ⅰ)求橢圓M的方程;
(2)設(shè)過右焦點F且與直線AB垂直的直線交橢圓M于C,D,求|AB| + |CD|的最小
值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:河北省2009-2010屆高三押題卷數(shù)學(xué)試卷文 題型:解答題
設(shè)橢圓M: (a>b>0)的離心率為
(a>b>0)的離心率為 ,長軸長為
,長軸長為 ,設(shè)過右焦點F傾
,設(shè)過右焦點F傾
斜角為 的直線交橢圓M于A,B兩點。
的直線交橢圓M于A,B兩點。
(Ⅰ)求橢圓M的方程;
(2)設(shè)過右焦點F且與直線AB垂直的直線交橢圓M于C,D,求|AB| + |CD|的最小
值。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com