
【題目】如圖,空間直角坐標系中,四棱錐![]() 的底面是邊長為
的底面是邊長為![]() 的正方形,且底面在
的正方形,且底面在![]() 平面內,點
平面內,點![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 平面
平面![]() ,側棱
,側棱![]() 與底面所成角為45°;
與底面所成角為45°;
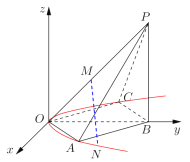
(1)若![]() 是頂點在原點,且過
是頂點在原點,且過![]() 、
、![]() 兩點的拋物線上的動點,試給出
兩點的拋物線上的動點,試給出![]() 與
與![]() 滿足的關系式;
滿足的關系式;
(2)若![]() 是棱
是棱![]() 上的一個定點,它到平面
上的一個定點,它到平面![]() 的距離為
的距離為![]() (
(![]() ),寫出
),寫出![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]() ,并求
,并求![]() 的最小值;
的最小值;
(3)是否存在一個實數![]() (
(![]() ),使得當
),使得當![]() 取得最小值時,異面直線
取得最小值時,異面直線![]() 與
與![]() 互相垂直?請說明理由;
互相垂直?請說明理由;
【答案】(1)![]() ;(2)
;(2)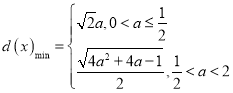 ;(3)
;(3)![]() .
.
【解析】
(1)根據題意,求出點![]() 的坐標,代入拋物線方程,即可得出
的坐標,代入拋物線方程,即可得出![]() 與
與![]() 的關系式;
的關系式;
(2)設點![]() 和
和![]() 的坐標,根據兩點間的距離公式,利用二次函數的基本性質,即可得出函數
的坐標,根據兩點間的距離公式,利用二次函數的基本性質,即可得出函數![]() 的最小值;
的最小值;
(3)由(2)可知,當![]() 時,當
時,當![]() 取得最小值時,求得
取得最小值時,求得![]() ,由異面直線
,由異面直線![]() 與
與![]() 垂直時,
垂直時,![]() ,代入即可求出
,代入即可求出![]() 的值.
的值.
(1)由四棱錐![]() 是底面邊長為
是底面邊長為![]() 的正方形,則
的正方形,則![]() ,
,
可設![]() 與
與![]() 所滿足的關系式為
所滿足的關系式為![]() ,將點
,將點![]() 橫坐標和豎坐標代入該方程得
橫坐標和豎坐標代入該方程得![]() ,
,
解得![]() ,因此,
,因此,![]() 與
與![]() 所滿足的關系式為
所滿足的關系式為![]() ;
;
(2)設點![]() ,
,![]() ,
,
則![]() .
.
令![]() ,設
,設![]() ,對稱軸為直線
,對稱軸為直線![]() .
.
①當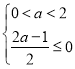 時,即當
時,即當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ,此時
,此時![]() ;
;
②當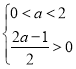 時,即當
時,即當![]() 時,此時函數
時,此時函數![]() 在
在![]() 取得最小值,即
取得最小值,即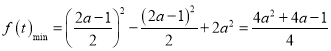 ,
,
此時![]() .
.
因此,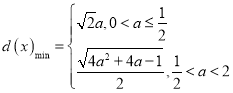 ;
;
(3)當![]() 時,此時點
時,此時點![]() 與原點重合,則直線
與原點重合,則直線![]() 與
與![]() 為相交直線,不符;
為相交直線,不符;
當![]() 時,則當
時,則當![]() 取最小值時,
取最小值時,![]() ,
,
當異面直線![]() 與
與![]() 垂直時,
垂直時,![]() ,即
,即![]() ,化簡得
,化簡得![]() .
.
![]() ,解得
,解得![]() .
.


科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)![]() 是函數數
是函數數![]() 的導函數,記
的導函數,記![]() ,若
,若![]() 在區間
在區間![]() 上為單調函數,求實數a的取值范圍;
上為單調函數,求實數a的取值范圍;
(2)設實數![]() ,求證:對任意實數
,求證:對任意實數![]()
![]() ,總有
,總有![]() 成立.
成立.
附:簡單復合函數求導法則為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若動點![]() 到定點
到定點![]() 與定直線
與定直線![]() 的距離之和為4.
的距離之和為4.
(1)求點![]() 的軌跡方程,并畫出方程的曲線草圖.
的軌跡方程,并畫出方程的曲線草圖.
(2)記(1)得到的軌跡為曲線![]() ,若曲線
,若曲線![]() 上恰有三對不同的點關于點
上恰有三對不同的點關于點![]() 對稱,求
對稱,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩個三口之家,共![]() 個大人,
個大人,![]() 個小孩,約定星期日乘紅色、白色兩輛轎車結伴郊游,每輛車最多乘坐
個小孩,約定星期日乘紅色、白色兩輛轎車結伴郊游,每輛車最多乘坐![]() 人,其中兩個小孩不能獨坐一輛車,則不同的乘車方法種數是_____.
人,其中兩個小孩不能獨坐一輛車,則不同的乘車方法種數是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是指大氣中直徑小于或等于
是指大氣中直徑小于或等于![]() 微米的顆粒物,也稱為可入肺顆粒物.雖然
微米的顆粒物,也稱為可入肺顆粒物.雖然![]() 只是地球大氣成分中含量很少的組分,但它對空氣質量和能見度等有重要的影響.我國
只是地球大氣成分中含量很少的組分,但它對空氣質量和能見度等有重要的影響.我國![]() 標準如下表所示.我市環保局從市區四個監測點2018年全年每天的
標準如下表所示.我市環保局從市區四個監測點2018年全年每天的![]() 監測數據中隨機抽取
監測數據中隨機抽取![]() 天的數據作為樣本,監測值如莖葉圖如圖所示.
天的數據作為樣本,監測值如莖葉圖如圖所示.
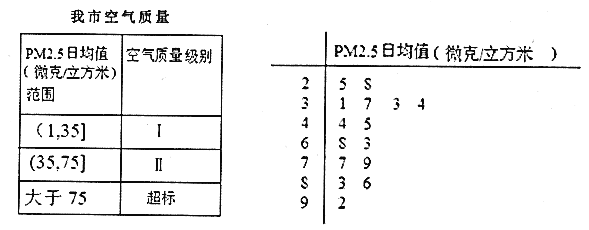
(Ⅰ)求這![]() 天數據的平均值;
天數據的平均值;
(Ⅱ)從這![]() 天的數據中任取
天的數據中任取![]() 天的數據,記表示其中空氣質量達到一級的天數
天的數據,記表示其中空氣質量達到一級的天數![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)以![]() 天的
天的![]() 日均值來估計一年的空氣質量情況,則一年(按
日均值來估計一年的空氣質量情況,則一年(按![]() 天計算)中大約有多少天的空氣質量達到一級.
天計算)中大約有多少天的空氣質量達到一級.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com