
【題目】已知正項等比數列![]() ,等差數列
,等差數列![]() 滿足
滿足![]() ,且
,且![]() 是
是![]() 與
與![]() 的等比中項.
的等比中項.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,分別是橢圓
,分別是橢圓![]() 的左、右焦點.
的左、右焦點.
(1)若點![]() 是第一象限內橢圓上的一點,
是第一象限內橢圓上的一點, ![]() ,求點
,求點![]() 的坐標;
的坐標;
(2)設過定點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,且
,且![]() 為銳角(其中
為銳角(其中![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點
的中點
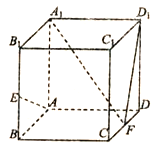
(1)求證:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 面
面![]() ,若存在,試確定
,若存在,試確定![]() 的值,若不存在說明理由;
的值,若不存在說明理由;
(3)在(2)的條件下,求面![]() 與面
與面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲同學寫出三個不等式:![]() :
:![]() ,
,![]() :
:![]() ,
,![]() :
:![]() ,然后將
,然后將![]() 的值告訴了乙、丙、丁三位同學,要求他們各用一句話來描述,以下是甲、乙、丙、丁四位同學的描述:
的值告訴了乙、丙、丁三位同學,要求他們各用一句話來描述,以下是甲、乙、丙、丁四位同學的描述:
乙:![]() 為整數;
為整數;
丙:![]() 是
是![]() 成立的充分不必要條件;
成立的充分不必要條件;
丁:![]() 是
是![]() 成立的必要不充分條件;
成立的必要不充分條件;
甲:三位同學說得都對,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點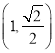 ,且兩個焦點的坐標分別為
,且兩個焦點的坐標分別為![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 為
為![]() 上的三個不同的點,
上的三個不同的點, ![]() 為坐標原點,且
為坐標原點,且![]() ,求證:四邊形
,求證:四邊形![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com