
【題目】在正方體![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點
的中點
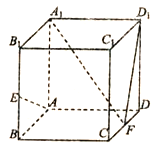
(1)求證:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 面
面![]() ,若存在,試確定
,若存在,試確定![]() 的值,若不存在說明理由;
的值,若不存在說明理由;
(3)在(2)的條件下,求面![]() 與面
與面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)詳見解析(2)存在,![]() (3)
(3)![]()
【解析】
(1) 取AB中點N,連接A1N,FN,可證得AE垂直于A1N,而A1NFD是平行四邊形,可得到AE垂直于![]() ,再由A1D1 AE可得到線面垂直;(2)取A1B1中點G,取GB1中點M,連接GB,ME,MC1,通過證明線線平行即
,再由A1D1 AE可得到線面垂直;(2)取A1B1中點G,取GB1中點M,連接GB,ME,MC1,通過證明線線平行即![]() ME可得到線面平行;(3)建立坐標系,求得兩個面的法向量,先得到余弦值,進而得到二面角的正弦值.
ME可得到線面平行;(3)建立坐標系,求得兩個面的法向量,先得到余弦值,進而得到二面角的正弦值.
(1)證明:取AB中點N,連接A1N,FN,
在正方體AC1中,AN![]() FD,所以四邊形ANFD為平行四邊形,AD
FD,所以四邊形ANFD為平行四邊形,AD![]() FN,
FN,
因為A1D1![]() AD,所以A1D1
AD,所以A1D1![]() FN,所以四邊形A1NFD1為平行四邊形,A1N
FN,所以四邊形A1NFD1為平行四邊形,A1N![]() FD1
FD1
在正方形A1B1BA中,RtEBA≌RtNAA1,所以∠EAB=∠NA1A
因為∠A1NA +∠NA1A=90°所以∠A1NA +∠EAB =90°,AEA1N,AE FD1
A1D1面A1B1BA,AE面A1B1BA,所以A1D1 AE,所以AE面A1FD1。
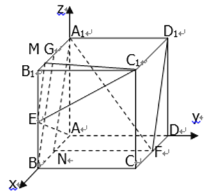
(2) 取A1B1中點G,取GB1中點M,連接GB,ME,MC1,
A1G![]() BN,所以四邊形A1GBN為平行四邊形,A1N
BN,所以四邊形A1GBN為平行四邊形,A1N![]() BG
BG
E為B1B的中點,M點為A1B1的四等分點,
所以EM∥BG,EM∥FD1
FD1面C1ME,EM面C1ME,所以D1F//面C1ME,
此時![]() =
=![]()
(3)如圖分別以AB、AD、AA1為x、y、z軸建立空間坐標系,
則E(2,0,1),C1(2,2,2),M(![]() ,0,2), A1(0,0,2), D1(0,2,2), F(1,2,0)
,0,2), A1(0,0,2), D1(0,2,2), F(1,2,0)
![]() =(
=(![]() ,2,0)
,2,0) ![]() =(0,2,1)
=(0,2,1) ![]() =(0,2,0)
=(0,2,0) ![]() =(-1,0,2)
=(-1,0,2)
設面MEC1的法向量為![]() =(x,y,z)
=(x,y,z)
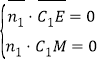 得
得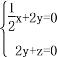 令y=1,則x=4,z=2,
令y=1,則x=4,z=2, ![]() =(4,1,2)
=(4,1,2)
設面![]() 的法向量為
的法向量為![]() =(x,y,z)
=(x,y,z)
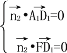 得
得![]() y=0令z=1,則x=2,
y=0令z=1,則x=2, ![]() =(2,0,1)
=(2,0,1)
cos<![]()
![]() >=
>=![]() =
=![]() =
=![]()
設面A1FD1與面C1ME所成二面角為θ,則|cosθ|=|cos<![]()
![]() >|=
>|=![]()
所以sinθ=![]() =
=![]()


科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人口老齡化的到來,我國的勞動力人口在不斷減少,“延遲退休”已經成為人們越來越關注的話題,為了解公眾對“延遲退休”的態度,某校課外研究性學習小組在某社區隨機抽取了50人進行調查,將調查情況進行整理后制成下表:
年齡 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人數 | 4 | 5 | 8 | 5 | 3 |
年齡 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人數 | 6 | 7 | 3 | 5 | 4 |
經調查年齡在[25,30),[55,60)的被調查者中贊成“延遲退休”的人數分別是3人和2人.現從這兩組的被調查者中各隨機選取2人,進行跟蹤調查.
(I)求年齡在[25,30)的被調查者中選取的2人都贊成“延遲退休”的概率;
(II)若選中的4人中,不贊成“延遲退休”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某船在![]() 處測得燈塔
處測得燈塔![]() 在其南偏東
在其南偏東![]() 方向上,該船繼續向正南方向行駛5海里到
方向上,該船繼續向正南方向行駛5海里到![]() 處,測得燈塔在其北偏東
處,測得燈塔在其北偏東![]() 方向上,然后該船向東偏南
方向上,然后該船向東偏南![]() 方向行駛2海里到
方向行駛2海里到![]() 處,此時船到燈塔
處,此時船到燈塔![]() 的距離為多少海里( )
的距離為多少海里( )
A.![]() 千米B.
千米B.![]() 千米C.6千米D.5千米
千米C.6千米D.5千米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,且
,且![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設![]() ,
,![]() ,連接
,連接![]() 并延長,與軌跡
并延長,與軌跡![]() 交于另一點
交于另一點![]() ,點
,點![]() 是
是![]() 中點,
中點,![]() 是坐標原點,記
是坐標原點,記![]() 與
與![]() 的面積之和為
的面積之和為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等比數列![]() 的公比為
的公比為![]() ,其前
,其前![]() 項和為
項和為![]() ,前
,前![]() 項之積為
項之積為![]() ,并且滿足條件:
,并且滿足條件:![]() ,
,![]() ,
,![]() ,下列結論中正確的是( )
,下列結論中正確的是( )
A. ![]() B.
B. ![]()
C. ![]() 是數列
是數列![]() 中的最大值 D. 數列
中的最大值 D. 數列![]() 無最小值
無最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種蔬菜從1月1日起開始上市,通過市場調查,得到該蔬菜種植成本![]() (單位:元/
(單位:元/![]() )與上市時間
)與上市時間![]() (單位:10天)的數據如下表:
(單位:10天)的數據如下表:
時間 | 5 | 11 | 25 |
種植成本 | 15 | 10.8 | 15 |
(1)根據上表數據,從下列函數:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),選取一個合適的函數模型描述該蔬菜種植成本
),選取一個合適的函數模型描述該蔬菜種植成本![]() 與上市時間
與上市時間![]() 的變化關系;
的變化關系;
(2)利用你選取的函數模型,求該蔬菜種植成本最低時的上市時間及最低種植成本.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別是△ABC的內角A,B,C的對邊,若△ABC的周長為2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,則a= ( )
sin A,則a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根據正弦定理把![]() 轉化為邊的關系,進而根據△ABC的周長,聯立方程組,可求出a的值.
轉化為邊的關系,進而根據△ABC的周長,聯立方程組,可求出a的值.
根據正弦定理,![]() 可化為
可化為![]()
∵△ABC的周長為![]() ,
,
∴聯立方程組![]() ,
,
解得a=2.
故選:B
【點睛】
(1)在三角形中根據已知條件求未知的邊或角時,要靈活選擇正弦、余弦定理進行邊角之間的轉化,以達到求解的目的.
(2)求角的大小時,在得到角的某一個三角函數值后,還要根據角的范圍才能確定角的大小,這點容易被忽視,解題時要注意.
【題型】單選題
【結束】
7
【題目】已知數列{an}中,an=n2-kn(n∈N*),且{an}單調遞增,則k的取值范圍是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com