
【題目】已知數列![]() 的前
的前![]() 項和
項和![]() 滿足,
滿足,![]() .數列
.數列![]() 的前
的前![]() 項和為
項和為![]() ,則滿足
,則滿足![]() 的最小的
的最小的![]() 值為______.
值為______.
【答案】7
【解析】
根據題意,將Sn=3an﹣2變形可得Sn﹣1=3an﹣1﹣2,兩式相減變形,并令n=1求出a1的值,即可得數列{an}是等比數列,求得數列{an}的通項公式,再由錯位相減法求出Tn的值,利用Tn>100,驗證分析可得n的最小值,即可得答案.
根據題意,數列{an}滿足Sn=3an﹣2,①
當n≥2時,有Sn﹣1=3an﹣1﹣2,②,
①﹣②可得:an=3an﹣3an﹣1,變形可得2an=3an﹣1,
當n=1時,有S1=a1=3a1﹣2,解可得a1=1,
則數列{an}是以a1=1為首項,公比為![]() 的等比數列,則an=(
的等比數列,則an=(![]() )n﹣1,
)n﹣1,
數列{nan}的前n項和為Tn,則Tn=1+2![]() 3×(
3×(![]() )2+……+n×(
)2+……+n×(![]() )n﹣1,③
)n﹣1,③
則有![]() Tn
Tn![]() 2×(
2×(![]() )2+3×(
)2+3×(![]() )3+……+n×(
)3+……+n×(![]() )n,④
)n,④
③﹣④可得:![]() Tn=1+(
Tn=1+(![]() )+(
)+(![]() )2+……×(
)2+……×(![]() )n﹣1﹣n×(
)n﹣1﹣n×(![]() )n=﹣2(1
)n=﹣2(1![]() )﹣n×(
)﹣n×(![]() )n,
)n,
變形可得:Tn=4+(2n﹣4)×(![]() )n,
)n,
若Tn>100,即4+(2n﹣4)×(![]() )n>100,
)n>100,
分析可得:n≥7,故滿足Tn>100的最小的n值為7;
故答案為:7.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中取兩個定點
中取兩個定點![]() ,
,![]() ,再取兩個動點
,再取兩個動點![]() ,
,![]() ,且
,且![]() .
.
(1)求直線![]() 與
與![]() 的交點
的交點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過![]() 的直線與軌跡
的直線與軌跡![]() 交于
交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸且與軌跡
軸且與軌跡![]() 交于另一點
交于另一點![]() ,
,![]() 為軌跡
為軌跡![]() 的右焦點,若
的右焦點,若![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在![]() 實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖,記綜合評分為80分及以上的花苗為優質花苗.
實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖,記綜合評分為80分及以上的花苗為優質花苗.

(1)用樣本估計總體,以頻率作為概率,若在![]() 兩塊實驗地隨機抽取3株花苗,求所抽取的花苗中優質花苗數的分布列和數學期望;
兩塊實驗地隨機抽取3株花苗,求所抽取的花苗中優質花苗數的分布列和數學期望;
(2)填寫下面的列聯表,并判斷是否有99%的把握認為優質花苗與培育方法有關.
優質花苗 | 非優質花苗 | 合計 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合計 |
附:下面的臨界值表僅供參考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(參考公式: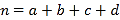 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某北方村莊4個草莓基地,采用水培陽光栽培方式種植的草莓個大味美,一上市便成為消費者爭相購買的對象.光照是影響草莓生長的關鍵因素,過去50年的資料顯示,該村莊一年當中12個月份的月光照量X(小時)的頻率分布直方圖如下圖所示(注:月光照量指的是當月陽光照射總時長).
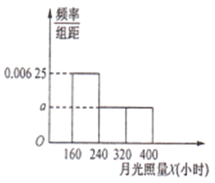
(1)求月光照量![]() (小時)的平均數和中位數;
(小時)的平均數和中位數;
(2)現準備按照月光照量來分層抽樣,抽取一年中的4個月份來比較草莓的生長狀況,問:應在月光照量![]() ,
,![]() ,
,![]() 的區間內各抽取多少個月份?
的區間內各抽取多少個月份?
(3)假設每年中最熱的5,6,7,8,9,10月的月光照量![]() 是大于等于240小時,且6,7,8月的月光照量
是大于等于240小時,且6,7,8月的月光照量![]() 是大于等于320小時,那么,從該村莊2018年的5,6,7,8,9,10這6個月份之中隨機抽取2個月份的月光照量進行調查,求抽取到的2個月份的月光照量
是大于等于320小時,那么,從該村莊2018年的5,6,7,8,9,10這6個月份之中隨機抽取2個月份的月光照量進行調查,求抽取到的2個月份的月光照量![]() (小時)都不低于320的概率.
(小時)都不低于320的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知m,n是兩條不同的直線,![]() ,
,![]() 是兩個不同的平面,給出下列命題:
是兩個不同的平面,給出下列命題:
①若![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,
,![]() ,則
,則![]() 或
或![]() ;
;
③若![]() ,
,![]() ,
,![]() ,則
,則![]() 或
或![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() 且
且![]() ;
;
其中正確命題的序號是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() ,直線
,直線![]() 過橢圓的
過橢圓的![]() 左焦點.
左焦點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() 是橢圓
是橢圓![]() 上的兩個動點,
上的兩個動點,![]() 的平分線在
的平分線在![]() 軸上,
軸上,![]() .試判斷直線
.試判斷直線![]() 是否過定點,若過定點,求出定點坐標;若不過定點,請說明理由.
是否過定點,若過定點,求出定點坐標;若不過定點,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com