
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() ,直線
,直線![]() 過橢圓的
過橢圓的![]() 左焦點.
左焦點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() 是橢圓
是橢圓![]() 上的兩個動點,
上的兩個動點,![]() 的平分線在
的平分線在![]() 軸上,
軸上,![]() .試判斷直線
.試判斷直線![]() 是否過定點,若過定點,求出定點坐標;若不過定點,請說明理由.
是否過定點,若過定點,求出定點坐標;若不過定點,請說明理由.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某品牌經銷商在一廣場隨機采訪男性和女性用戶各50名,其中每天玩微信超過6小時的用戶列為“微信控”,否則稱其為“非微信控”,調查結果如下:
微信控 | 非微信控 | 合計 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合計 | 56 | 44 | 100 |
(1)根據以上數據,能否有95%的把握認為“微信控”與“性別”有關?
(2)現從調查的女性用戶中按分層抽樣的方法選出5人,求所抽取的5人中“微信控”和“非微信控”的人數;
(3)從(2)中抽取的5位女性中,再隨機抽取3人贈送禮品,試求抽取3人中恰有2人位“微信控”的概率.
參考公式:  ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在我們的教材必修一中有這樣一個問題,假設你有一筆資金,現有三種投資方案供你選擇,這三種方案的回報如下:
方案一:每天回報![]() 元;
元;
方案二:第一天回報![]() 元,以后每天比前一天多回報
元,以后每天比前一天多回報![]() 元;
元;
方案三:第一天回報![]() 元,以后每天的回報比前一天翻一番.
元,以后每天的回報比前一天翻一番.
記三種方案第![]() 天的回報分別為
天的回報分別為![]() ,
,![]() ,
,![]() .
.
(1)根據數列的定義判斷數列![]() ,
,![]() ,
,![]() 的類型,并據此寫出三個數列的通項公式;
的類型,并據此寫出三個數列的通項公式;
(2)小王準備做一個為期十天的短期投資,他應該選擇哪一種投資方案?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表列出了10名5至8歲兒童的體重x(單位kg)(這是容易測得的)和體積y(單位dm3)(這是難以測得的),繪制散點圖發現,可用線性回歸模型擬合y與x的關系:
體重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
體積y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y關于x的線性回歸方程![]() (系數精確到0.01);
(系數精確到0.01);
(2)某5歲兒童的體重為13.00kg,估測此兒童的體積.
附注:參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,137×14=1918.00.
,137×14=1918.00.
參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為: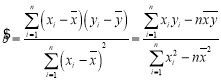 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為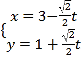 (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() 的坐標為(3,1),求
的坐標為(3,1),求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com