
分析 (Ⅰ)函數f(x)的定義域為R,且f(x)是奇函數,故f(0)=0,解得a值;
(Ⅱ) 任取x1<x2,作差判斷f(x1)與f(x2)的大小,根據函數單調性的定義,可得函數f(x)在R上的單調性;
(Ⅲ)若對任意的x∈R,不等式f(x2-x)+f(2x2-k)>0恒成立,
解答 解:(Ⅰ)∵函數f(x)的定義域為R,且f(x)是奇函數,
∴f(0)=0,解得a=1
此時f(x)=2x-2-x,滿足f(-x)=-f(x),即f(x)是奇函數.
∴a=1. …(4分)
(Ⅱ) 任取x1<x2,則${2}^{{x}_{1}}<{2}^{{x}_{2}}$,${2}^{{-x}_{1}}>{2}^{-{x}_{2}}$,
于是f(x1)-f(x2)=(${2}^{{x}_{1}}-{2}^{-{x}_{1}}$)-(${2}^{{x}_{2}}-{2}^{-{x}_{2}}$)=${2}^{{x}_{1}}-{2}^{{x}_{2}}$-(${2}^{{-x}_{1}}-{2}^{-{x}_{2}}$)<0,
即f(x1)<f(x2),故函數f(x)在R上是增函數.…(8分)
(Ⅲ)不等式f(x2-x)+f(2x2-k)>0可化為:f(x2-x)>-f(2x2-k)=f(-2x2+k)
又由f(x)在R上是增函數,
得x2-x>-2x2+k,
即k<3x2-x對任意的x∈R恒成立
∵當x=$\frac{1}{6}$時,3x2-取最小值$-\frac{1}{12}$,
∴k<$-\frac{1}{12}$.…(12分)
點評 本題考查的知識點是函數恒成立問題,函數的奇偶性,函數的單調性,難度中檔.


 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:選擇題
| A. | (0,2) | B. | ( $\sqrt{2}$,2) | C. | (2,4) | D. | (2,2 $\sqrt{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,$\sqrt{3}$) | B. | (-$\sqrt{3}$,-$\frac{\sqrt{3}}{3}$) | C. | (-∞,0)∪($\sqrt{3}$,+∞) | D. | (-$\sqrt{3}$,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
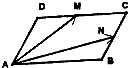 如圖所示,在平行四邊形ABCD中,M,N分別為DC,BC的中點,已知$\overrightarrow{AN}=\overrightarrow b,\overrightarrow{AM}=\overrightarrow c,\overrightarrow{AD}用\overrightarrow c,\overrightarrow b$表示為$\overrightarrow{AD}$=$\frac{4}{3}\overrightarrow{c}-\frac{2}{3}\overrightarrow{b}$.
如圖所示,在平行四邊形ABCD中,M,N分別為DC,BC的中點,已知$\overrightarrow{AN}=\overrightarrow b,\overrightarrow{AM}=\overrightarrow c,\overrightarrow{AD}用\overrightarrow c,\overrightarrow b$表示為$\overrightarrow{AD}$=$\frac{4}{3}\overrightarrow{c}-\frac{2}{3}\overrightarrow{b}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com