
【題目】如圖,在矩形![]() 中,已知
中,已知![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() ,將四邊形
,將四邊形![]() 沿
沿![]() 折起,使點
折起,使點![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直線
在直線![]() 上.
上.
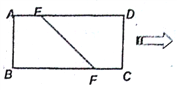
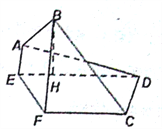
(I)求證: ![]() ;
;
(II)求點![]() 到平面
到平面![]() 的距離;
的距離;
(III)求直線![]() 與平面
與平面![]() 所成的正弦值.
所成的正弦值.
【答案】(1)見解析(2)2(3)![]()
【解析】試題分析:
(1)由折疊關系可得![]() 平面
平面![]() ,
, ![]() .
.
(2)利于題意結合勾股定理列方程組,求解可得點![]() 到平面
到平面![]() 的距離為2;
的距離為2;
(3)做出直線與平面所成的角,結合(1)(2)的結論可得直線![]() 與平面
與平面![]() 所成的正弦值為
所成的正弦值為![]() .
.
試題解析:
解:(1)由于![]() 平面
平面![]() ,
, ![]() ,又由于
,又由于![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,
, ![]() .
.
法一:(2)設![]() ,
, ![]() ,過
,過![]() 作
作![]() 垂直
垂直![]() 于
于![]() ,
,
因線段![]() ,
, ![]() 在翻折過程中長度不變,根據勾股定理:
在翻折過程中長度不變,根據勾股定理:
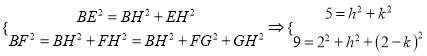 ,可解得
,可解得![]() ,
,
![]() 線段
線段![]() 長度為
長度為![]() ,即點
,即點![]() 的平面
的平面![]() 的距離為
的距離為![]() .
.
(2)延長![]() 交
交![]() 于點
于點![]() ,因為
,因為![]()
點![]() 到平面
到平面![]() 的距離為點
的距離為點![]() 到平面
到平面![]() 距離的
距離的![]() ,
,
![]() 點
點![]() 平面
平面![]() 的距離為
的距離為![]() ,而
,而![]() ,
,
直線![]() 與平面
與平面![]() 新角的正弦值為
新角的正弦值為![]() .
.
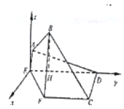
法二:(2)如圖,過點![]() 作
作![]() ,過點
,過點![]() 作
作![]() 平面
平面![]() ,分別以
,分別以![]() 、
、![]() 、
、![]() 為
為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系,設點
軸建立空間直角坐標系,設點![]() ,由于
,由于![]() ,
,
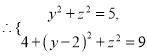 解得
解得![]() 于是
于是![]() ,所以線段
,所以線段![]() 的長度為
的長度為![]() .
.
即點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
(3)從而![]() ,故
,故![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,設直線
,設直線![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ,
,
則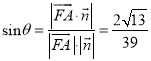


科目:高中數學 來源: 題型:
【題目】f(x)是定義在R上的奇函數,對x,y∈R都有f(x+y)=f(x)+f(y),且當x>0時,f(x)<0,f(-1)=2.
(1)求證:f(x)為奇函數;
(2)求證:f(x)是R上的減函數;
(3)求f(x)在[-2,4]上的最值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:t)和年利潤
(單位:t)和年利潤![]() (單位:千元)的影響.對近8年的年宣傳費
(單位:千元)的影響.對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() (i=1,2,…,8)數據作了初步處理,得到右面的散點圖及一些統計量的值.
(i=1,2,…,8)數據作了初步處理,得到右面的散點圖及一些統計量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
, ![]()
(1)根據散點圖判斷, ![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知這種產品的年利潤![]() 與
與![]() 的關系為
的關系為![]() .根據(2)的結果回答下列問題:
.根據(2)的結果回答下列問題:
①年宣傳費![]() =49時,年銷售量及年利潤的預報值是多少?
=49時,年銷售量及年利潤的預報值是多少?
②年宣傳費![]() 為何值時,年利潤的預報值最大?
為何值時,年利潤的預報值最大?
附:對于一組數據![]() ,
, ![]() …,
…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況,在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當20≤x≤200時,車流速度v是車流密度x的一次函數.
(Ⅰ)當0≤x≤200時,求函數v(x)的表達式;
(Ⅱ)當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)f(x)=xv(x)可以達到最大,并求出最大值.(精確到1輛/小時).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5名男生4名女生站成一排,求滿足下列條件的排法:
(1)女生都不相鄰有多少種排法?
(2)男生甲、乙、丙排序一定(只考慮位置的前后順序),有多少種排法?
(3)男甲不在首位,男乙不在末位,有多少種排法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,直線![]() 的參數方程為
的參數方程為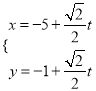 (其中
(其中![]() 為參數),現以坐標原點為極點,
為參數),現以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 和曲線
和曲線![]() 的普通方程;
的普通方程;
(2)已知點![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com