
【題目】f(x)是定義在R上的奇函數,對x,y∈R都有f(x+y)=f(x)+f(y),且當x>0時,f(x)<0,f(-1)=2.
(1)求證:f(x)為奇函數;
(2)求證:f(x)是R上的減函數;
(3)求f(x)在[-2,4]上的最值.
科目:高中數學 來源: 題型:
【題目】已知,△ABC的三個內角為A,B,C,m=(sin B+sin C,0),n=(0,sin A)且
|m|2-|n|2=sin Bsin C.
(1)求角A的大小
(2)求sin B+sin C的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,建立平面直角坐標系xOy,x軸在地平面上,y軸垂直于地平面,單位長度為1千米.某炮位于坐標原點.已知炮彈發射后的軌跡在方程y=kx-![]() (1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.
(1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.

(1)求炮的最大射程;
(2)設在第一象限有一飛行物(忽略其大小),其飛行高度為3.2千米,試問它的橫坐標a不超過多少時,炮彈可以擊中它?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·雅安高一檢測)已知函數f(x)=2x的定義域是[0,3],設g(x)=f(2x)-f(x+2),
(1)求g(x)的解析式及定義域;
(2)求函數g(x)的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以
為參數),在以![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,射線
軸的正半軸為極軸的極坐標系中,射線![]() ,與
,與![]() ,
,![]() 各有一個交點,當
各有一個交點,當![]() 時,這兩個交點間的距離為2,當
時,這兩個交點間的距離為2,當![]() ,這兩個交點重合.
,這兩個交點重合.
(1)分別說明![]() ,
,![]() 是什么曲線,并求出
是什么曲線,并求出![]() 與
與![]() 的值;
的值;
(2)設當![]() 時,
時,![]() 與
與![]() ,
,![]() 的交點分別為
的交點分別為![]() ,當
,當![]() ,
,![]() 與
與![]() ,
,![]() 的交點分別為
的交點分別為![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,且當
上的奇函數,且當![]() 時,
時, ![]() .
.

(1)求函數![]() 的解析式;
的解析式;
(2)現已畫出函數![]() 在
在![]() 軸左側的圖象,如圖所示,請補全完整函數
軸左側的圖象,如圖所示,請補全完整函數![]() 的圖象;
的圖象;
(3)根據(2)中畫出的函數圖像,直接寫出函數![]() 的單調區間.
的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上, ![]() ,
, ![]() ,過
,過![]() 與坐標軸不垂直的直線
與坐標軸不垂直的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,
兩點, ![]() 為
為![]() ,
, ![]() 的中點.
的中點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知點![]() ,且
,且![]() ,求直線
,求直線![]() 所在的直線方程.
所在的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
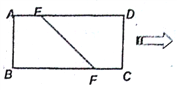
【題目】如圖,在矩形![]() 中,已知
中,已知![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() ,將四邊形
,將四邊形![]() 沿
沿![]() 折起,使點
折起,使點![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直線
在直線![]() 上.
上.
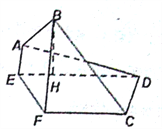
(I)求證: ![]() ;
;
(II)求點![]() 到平面
到平面![]() 的距離;
的距離;
(III)求直線![]() 與平面
與平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com