
【題目】已知命題p1:函數y=2x-2-x在R上為增函數,p2:函數y=2x+2-x在R上為減函數,則在命題q1:p1∨p2,q2:p1∧p2,q3:(p1)∨p2和q4:p1∧(p2)中,真命題是
A.q1,q3
B.q2,q3
C.q1,q4
D.q2,q4
科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足:對于任意的正整數
滿足:對于任意的正整數![]() ,
,![]() ,
,![]() ,且
,且![]() ,則稱該數列為“跳級數列”.
,則稱該數列為“跳級數列”.
(1)若數列![]() 為“跳級數列”,且
為“跳級數列”,且![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若數列![]() 為“跳級數列”,則對于任意一個大于
為“跳級數列”,則對于任意一個大于![]() 的質數
的質數![]() ,在數列
,在數列![]() 中總有一項是
中總有一項是![]() 的倍數;
的倍數;
(3)若![]() 為奇質數,則存在一個“跳級數列”
為奇質數,則存在一個“跳級數列”![]() ,使得數列
,使得數列![]() 中每一項都不是
中每一項都不是![]() 的倍數.
的倍數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車公司最近研發了一款新能源汽車,并在出廠前對100輛汽車進行了單次最大續航里程的測試。現對測試數據進行分析,得到如圖所示的頻率分布直方圖:

(1)估計這100輛汽車的單次最大續航里程的平均值(同一組中的數據用該組區間的中點值代表).
(2)根據大量的汽車測試數據,可以認為這款汽車的單次最大續航里程![]() 近似地服從正態分布
近似地服從正態分布![]() ,經計算第(1)問中樣本標準差
,經計算第(1)問中樣本標準差![]() 的近似值為50。用樣本平均數
的近似值為50。用樣本平均數![]() 作為
作為![]() 的近似值,用樣本標準差
的近似值,用樣本標準差![]() 作為
作為![]() 的估計值,現任取一輛汽車,求它的單次最大續航里程恰在250千米到400千米之間的概率.
的估計值,現任取一輛汽車,求它的單次最大續航里程恰在250千米到400千米之間的概率.
參考數據:若隨機變量服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
(3)某汽車銷售公司為推廣此款新能源汽車,現面向意向客戶推出“玩游戲,送大獎”活動,客戶可根據拋擲硬幣的結果,操控微型遙控車在方格圖上行進,若遙控車最終停在“勝利大本營”,則可獲得購車優惠券3萬元。已知硬幣出現正、反面的概率都是0.5方格圖上標有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,客戶每擲一次硬幣,遙控車向前移動一次。若擲出正面,遙控車向前移動一格(從![]() 到
到![]() )若擲出反面遙控車向前移動兩格(從
)若擲出反面遙控車向前移動兩格(從![]() 到
到![]() ),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第
),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第![]() 格的概率為P試證明
格的概率為P試證明![]() 是等比數列,并求參與游戲一次的顧客獲得優惠券金額的期望值。
是等比數列,并求參與游戲一次的顧客獲得優惠券金額的期望值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年1月3日嫦娥四號探測器成功實現人類歷史上首次月球背面軟著陸,我國航天事業取得又一重大成就,實現月球背面軟著陸需要解決的一個關鍵技術問題是地面與探測器的通訊聯系.為解決這個問題,發射了嫦娥四號中繼星“鵲橋”,鵲橋沿著圍繞地月拉格朗日![]() 點的軌道運行.
點的軌道運行.![]() 點是平衡點,位于地月連線的延長線上.設地球質量為M1,月球質量為M2,地月距離為R,
點是平衡點,位于地月連線的延長線上.設地球質量為M1,月球質量為M2,地月距離為R,![]() 點到月球的距離為r,根據牛頓運動定律和萬有引力定律,r滿足方程:
點到月球的距離為r,根據牛頓運動定律和萬有引力定律,r滿足方程:
![]() .
.
設![]() ,由于
,由于![]() 的值很小,因此在近似計算中
的值很小,因此在近似計算中![]() ,則r的近似值為
,則r的近似值為
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4,坐標系與參數方程】
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為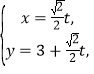 (t為參數),在以O為極點,
(t為參數),在以O為極點,![]() 軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為
軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為![]()
(Ⅰ)求直線![]() 的普通方程與曲線C的直角坐標方程;
的普通方程與曲線C的直角坐標方程;
(Ⅱ)若直線![]() 與
與![]() 軸的交點為P,直線
軸的交點為P,直線![]() 與曲線C的交點為A,B,求
與曲線C的交點為A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某媒體為調查喜愛娛樂節目![]() 是否與觀眾性別有關,隨機抽取了30名男性和30名女性觀眾,抽查結果用等高條形圖表示如圖:
是否與觀眾性別有關,隨機抽取了30名男性和30名女性觀眾,抽查結果用等高條形圖表示如圖:
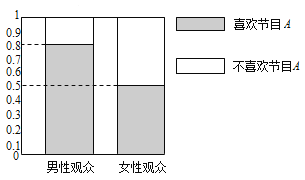
(1)根據該等高條形圖,完成下列![]() 列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節目
列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節目![]() 與觀眾性別有關?
與觀眾性別有關?

(2)從性觀眾中按喜歡節目![]() 與否,用分層抽樣的方法抽取5名做進一步調查.從這5名中任選2名,求恰有1名喜歡節目
與否,用分層抽樣的方法抽取5名做進一步調查.從這5名中任選2名,求恰有1名喜歡節目![]() 和1名不喜歡節目
和1名不喜歡節目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
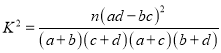 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com