
已知橢圓 經過點
經過點 ,且兩焦點與短軸的兩個端點的連線構成一正方形.
,且兩焦點與短軸的兩個端點的連線構成一正方形.
(1)求橢圓 的方程;
的方程;
(2)直線 與橢圓
與橢圓 交于
交于 ,
, 兩點,若線段
兩點,若線段 的垂直平分線經過點
的垂直平分線經過點 ,求
,求
( 為原點)面積的最大值.
為原點)面積的最大值.
(1) (2)
(2) 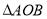 面積的最大值為
面積的最大值為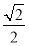 .
.
【解析】
試題分析:(1)由已知得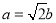 ,再根據橢圓經過點
,再根據橢圓經過點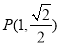 ,代入橢圓方程即可.
,代入橢圓方程即可.
(2)設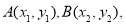
當直線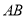 的斜率為
的斜率為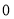 時,可得
時,可得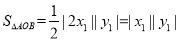 ,由
,由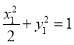 ,得到
,得到
 ;
;
當直線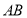 的斜率不為
的斜率不為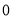 時,將
時,將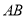 的方程為
的方程為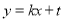 與橢圓方程聯立,
與橢圓方程聯立,
整理得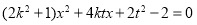 ,
,
由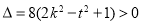 , 得到
, 得到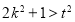
應用韋達定理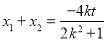 ,
,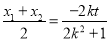 ,化簡得到
,化簡得到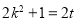
代入 ,得到
,得到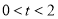 ;
;
通過確定原點到直線的距離為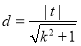 ,
,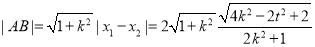 得到
得到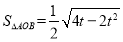 求其最值.
求其最值.
試題解析:(1)∵橢圓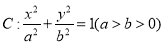 的兩焦點與短軸的兩個端點的連線構成正方形,∴
的兩焦點與短軸的兩個端點的連線構成正方形,∴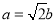 , ∴
, ∴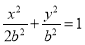 , 2分
, 2分
又∵橢圓經過點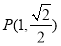 ,代入可得
,代入可得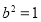 ,
,
∴故所求橢圓方程為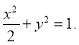 4分
4分
(2)設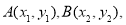 因為
因為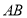 的垂直平分線通過點
的垂直平分線通過點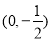 , 顯然直線
, 顯然直線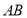 有斜率,
有斜率,
當直線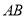 的斜率為
的斜率為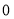 時,則
時,則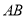 的垂直平分線為
的垂直平分線為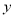 軸,此時
軸,此時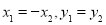
所以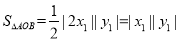 ,因為
,因為 ,所以
,所以
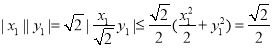
所以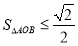 ,當且僅當
,當且僅當 時,
時,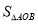 取得最大值為
取得最大值為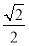 , 7分
, 7分
當直線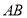 的斜率不為
的斜率不為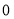 時,則設
時,則設 的方程為
的方程為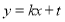
所以 ,代入得到
,代入得到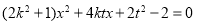 8分
8分
當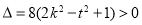 , 即
, 即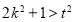
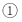
方程有兩個不同的解又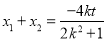 ,
,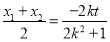 10分
10分
所以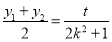 ,又
,又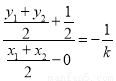 ,化簡得到
,化簡得到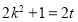
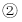
代入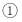 ,得到
,得到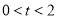 11分
11分
又原點到直線的距離為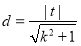
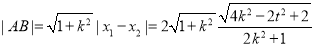
所以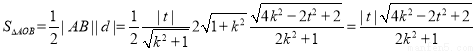
考慮到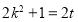 且
且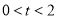 化簡得到
化簡得到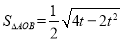 13分
13分
因為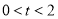 ,所以當
,所以當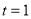 時,即
時,即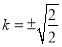 時,
時, 取得最大值
取得最大值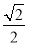 .
.
綜上,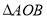 面積的最大值為
面積的最大值為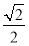 14分
14分
考點:橢圓的幾何性質,直線與圓錐曲線的位置關系,三角形面積公式.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源:2015屆吉林省吉林市高三第一次摸底考試理科數學試卷(解析版) 題型:選擇題
已知等差數列 的公差為 2,若前 17 項和為
的公差為 2,若前 17 項和為  ,則
,則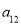 的值為( )
的值為( )
A.-10 B.8 C.4 D.12
查看答案和解析>>
科目:高中數學 來源:2015屆北京市海淀區高三上學期期中練習文科數學試卷(解析版) 題型:選擇題
設等差數列 的前
的前 項和為
項和為 .在同一個坐標系中,
.在同一個坐標系中,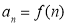 及
及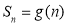 的部分圖象如圖所示,則( )
的部分圖象如圖所示,則( )

(A)當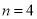 時,
時, 取得最大值
取得最大值
(B)當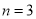 時,
時, 取得最大值
取得最大值
(C)當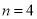 時,
時, 取得最小值
取得最小值
(D)當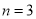 時,
時, 取得最小值
取得最小值
查看答案和解析>>
科目:高中數學 來源:2015屆北京市朝陽區高三上學期期中統一考試文科數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在
在 上的最大值與最小值.
上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省煙臺市高三統一質量檢測考試文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)全國第十二屆全國人民代表大會第二次會議和政協第十二屆全國委員會第二次會議,2014年3月在北京開幕.期間為了了解國企員工的工資收入狀況,從108名相關人員中用分層抽樣方法抽取若干人組成調研小組,有關數據見下表:(單位:人)
| 相關人數 | 抽取人數 |
一般職工 | 63 |
|
中層 | 27 |
|
高管 | 18 | 2 |
(1)求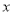 ,
,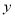 ;
;
(2)若從中層、高管抽取的人員中選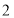 人,求這二人都來自中層的概率.
人,求這二人都來自中層的概率.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省煙臺市高三5月適應性訓練一文科數學試卷(解析版) 題型:解答題
設函數 (
( ),其圖象的兩個相鄰對稱中心的距離為
),其圖象的兩個相鄰對稱中心的距離為 .
.
(1)求函數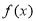 的解析式;
的解析式;
(2)若△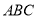 的內角為
的內角為 所對的邊分別為
所對的邊分別為 (其中
(其中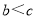 ),且
),且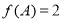 ,
,
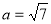 ,
, 面積為
面積為 ,求
,求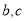 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com