【題目】把
個不同的球隨機地放入編號為1，2，…，
的個盒子內，求1號盒恰有
個球的概率．
【答案】
【解析】
法一：由題意知，把事件看成一次獨立試驗，其中放入1號盒的概率為
，
個球放入
個不同的盒子內相當于做次獨立重復試驗，由獨立重復試驗中事件
恰好發生
次的概率公式得到結果；
法二：根據題意，可知個不同的球任意放入個不同的盒子內，共有
個基本事件，再根據組合的應用求出1號盒內恰有
個球的結果數，最后利用古典概型可得出所求概率.
解法1：把1個球放入個不同的盒子內看成一次獨立試驗，
其中放人1號盒的概率為
，
這樣個球放入個不同的盒子內相當于做次獨立重復試驗，
由獨立重復試驗中事件恰好發生次的概率公式知，
1號盒恰有個球的概率為：
．
解法2：用古典概型把個不同的球任意放入個不同的盒子內，
共有個等可能的結果，
其中1號盒內恰有個球的結果數為
，
故所求概率為：
．
小學教材全測系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，某地區打算在一塊矩形地塊上修建一個牧場（ABCDEF圍成的封閉區域）用來養殖牛和羊，其中AF=1，AB=10，BC=4，CD=7（單位：百米），DEF是一段曲線形馬路.該牧場的核心區為等腰直角三角形MPQ所示區域，該區域用來養殖羊，其余區域養殖牛，且MP=PQ，牧場大門位于馬路DEF上的M處，一個觀察點P位于AB的中點處，為了能夠更好觀察動物的生活情況，現決定修建一條觀察通道，起點位于距離觀察點P處1百米的O點所示位置，終點位于Q處.如圖2所示，建立平面直角坐標系，若
滿足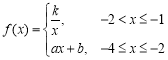
.
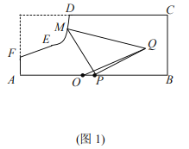
（1）求
的解析式；
（2）求觀察通道OQ長度的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設甲、乙、丙三臺機器是否需要照顧相互之間沒有影響．已知在某1 h內，甲、乙都需要照顧的概率為0.05，甲、丙都需要照顧的概率為0.1，乙、丙都需要照顧的概率為0.125．
（1）求甲、乙、丙每臺機器在這1 h內需要照顧的概率分別是多少？
（2）計算這1 h內至少有一臺機器需要照顧的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖1是某縣參加2007年高考的學生身高條形統計圖，從左到右的各條形圖表示學生人數依次記為A1、A2、…A10（如A2表示身高（單位：cm）在[150，155
內的人數]．圖2是統計圖1中身高在一定范圍內學生人數的一個算法流程圖．現要統計身高在160~180cm（含160cm，不含180cm）的學生人數，那么在流程圖中的判斷框內應填寫的條件是
A.i<6B.i<7C.i<8D.i<9
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設{an}是一個首項為2，公比為q（q
1）的等比數列，且3a1，2a2，a3成等差數列.
（1）求{an}的通項公式；
（2）已知數列{bn}的前n項和為Sn，b1=1，且
1（n≥2），求數列{an
bn}的前n項和Tn.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
，
）的周期為
，圖像的一個對稱中心為
，將函數
圖像上的所有點的橫坐標伸長為原來的2倍（縱坐標不變），在將所得圖像向右平移
個單位長度后得到函數
的圖像．
（1）求函數與的解析式；
（2）是否存在
，使得
，
，
按照某種順序成等差數列？若存在，請確定
的個數；若不存在，說明理由．
（3）求實數a與正整數n，使得
在
內恰有2013個零點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】著名數學家華羅庚先生曾說過：“數缺形時少直觀，形缺數時難入微數形結合百般好，隔裂分家萬事休.”在數學的學習和研究中，我們經常用函數的圖象來研究函數的性質，也經常用函數的解析式來琢磨函數的圖象的特征，如某體育品牌的LOGO為
，可抽象為如圖所示的軸對稱的優美曲線，下列函數中，其圖象大致可“完美”局部表達這條曲線的函數是( )
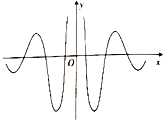
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
