
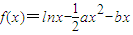 .
. 時,求f(x)的最大值;
時,求f(x)的最大值; ,(0<x≤3),其圖象上任意一點P(x,y)處切線的斜率k≤
,(0<x≤3),其圖象上任意一點P(x,y)處切線的斜率k≤ 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍; 代入函數解析式,求其導數,根據求解目標,這個導數在函數定義域內只有一個等于零的點,判斷這唯一的極值點是極大值點即可;
代入函數解析式,求其導數,根據求解目標,這個導數在函數定義域內只有一個等于零的點,判斷這唯一的極值點是極大值點即可; 恒成立,分離參數后轉化為函數的最值;
恒成立,分離參數后轉化為函數的最值;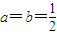 時,
時, ,
,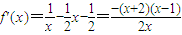 (2′)
(2′)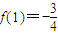 ,此即為最大值…(4分)
,此即為最大值…(4分)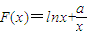 ,x∈(0,3],則有
,x∈(0,3],則有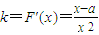 ≤
≤ ,在x∈(0,3]上恒成立,
,在x∈(0,3]上恒成立,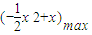 ,x∈(0,3],
,x∈(0,3],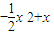 取得最大值
取得最大值 ,
, …(8分)
…(8分)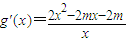 .
.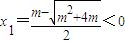 (舍去),
(舍去),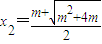 ,
, 既
既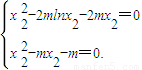
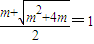 ,解得
,解得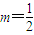 .…(12分)
.…(12分) ,由這個方程組求解m使用了構造函數通過函數的性質得到x2的方法也是值得仔細體會的技巧.
,由這個方程組求解m使用了構造函數通過函數的性質得到x2的方法也是值得仔細體會的技巧. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
(07年寧夏、 海南卷理)(12分)
設函數![]()
(I)若當![]() 時,
時,![]() 取得極值,求
取得極值,求![]() 的值,并討論
的值,并討論![]() 的單調性;
的單調性;
(II)若![]() 存在極值,求
存在極值,求![]() 的取值范圍,并證明所有極值之和大于
的取值范圍,并證明所有極值之和大于![]() .
.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省高三(奧班)10月月考理科數學試卷(解析版) 題型:解答題
選修4-5:不等式選講(本小題滿分10分)
設函數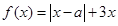 ,其中
,其中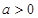 。
。
(Ⅰ)當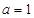 時,求不等式
時,求不等式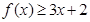 的解集;
的解集;
(Ⅱ)若不等式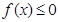 的解集為
的解集為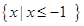 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年新人教版高三一輪復習單元測試(8)數學試卷 題型:解答題
(12分)(理)設函數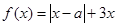 ,其中
,其中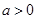 。
。
(Ⅰ)當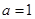 時,求不等式
時,求不等式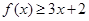 的解集;
的解集;
(Ⅱ)若不等式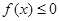 的解集為
的解集為 ,求a的值。
,求a的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com