
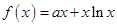 的圖象在點
的圖象在點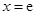 (
(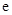 為自然對數的底數)處的切線斜率為3.
為自然對數的底數)處的切線斜率為3.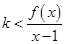 (Ⅰ)求實數
(Ⅰ)求實數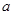 的值;
的值;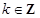 ,且 對任意
,且 對任意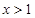 恒成立,求
恒成立,求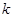 的最大值;
的最大值;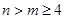 時,證明
時,證明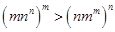 .
.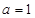 .(2)整數
.(2)整數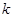 的最大值是3.(3)見解析
的最大值是3.(3)見解析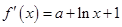 ,以及函數
,以及函數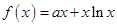 的圖像在點
的圖像在點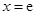 處的切線斜率為3,所以
處的切線斜率為3,所以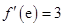 ,得a=1
,得a=1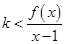 對任意
對任意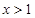 恒成立,即
恒成立,即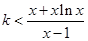 對任意
對任意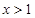 恒成立.構造新函數,利用導數來判定單調性求解最值。第三問中,由(2)知,
恒成立.構造新函數,利用導數來判定單調性求解最值。第三問中,由(2)知,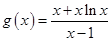 是
是 上的增函數,
上的增函數, 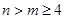 時,
時,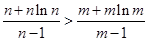
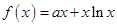 ,所以
,所以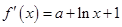 .…………………1分
.…………………1分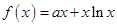 的圖像在點
的圖像在點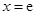 處的切線斜率為3,
處的切線斜率為3,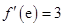 ,即
,即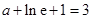 .所以
.所以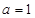 .……………………………2分
.……………………………2分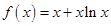 ,
,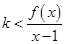 對任意
對任意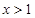 恒成立,即
恒成立,即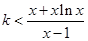 對任意
對任意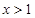 恒成立.………………………3分
恒成立.………………………3分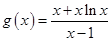 ,則
,則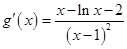 ,…………………………………4分
,…………………………………4分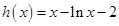
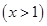 ,則
,則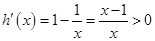 ,
,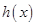 在
在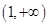 上單調遞增.……………5分
上單調遞增.……………5分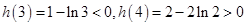 ,
,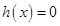 在
在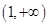 上存在唯一實根
上存在唯一實根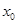 ,且滿足
,且滿足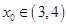 .
. ,即
,即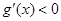 ,當
,當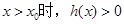 ,即
,即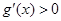 ,…6分
,…6分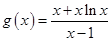 在
在 上單調遞減,在
上單調遞減,在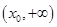 上單調遞增.
上單調遞增. .…7分
.…7分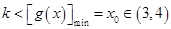 .故整數
.故整數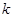 的最大值是3.……8分
的最大值是3.……8分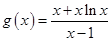 是
是 上的增函數,……………9分
上的增函數,……………9分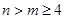 時,
時,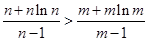 .………………10分
.………………10分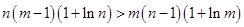 .整理,得
.整理,得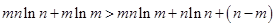 .
. ,所以
,所以 .
.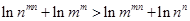 .即
.即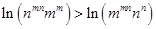 .所以
.所以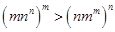 .
.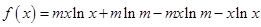 ,…………………………9分
,…………………………9分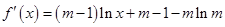 .……………………………10分
.……………………………10分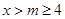 ,所以
,所以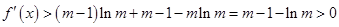 .
. 在
在 上單調遞增. 因為
上單調遞增. 因為 , 所以
, 所以 .
.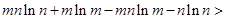
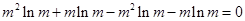 .
. .
.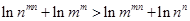 .即
.即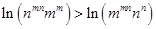 .
. 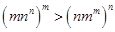 .
.

科目:高中數學 來源:不詳 題型:解答題
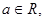 函數
函數 。
。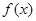 在區間
在區間 上最小值
上最小值 ;
; ,若關于
,若關于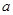 的方程
的方程 有兩個不同的實數解,求實數
有兩個不同的實數解,求實數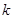 的取值范圍;
的取值范圍;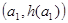 ,B
,B ,C
,C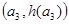 ,從左到右依次是函數
,從左到右依次是函數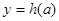 圖象上三點,且這三點不共線,求證:
圖象上三點,且這三點不共線,求證: 是鈍角三角形。
是鈍角三角形。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
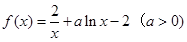 .
.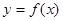 在點
在點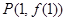 處的切線與直線
處的切線與直線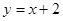 垂直,求函數
垂直,求函數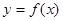 的單調區間;
的單調區間;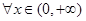 都有
都有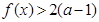 成立,試求
成立,試求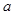 的取值范圍;
的取值范圍;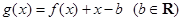 .當
.當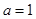 時,函數
時,函數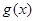 在區間
在區間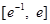 上有兩個零點,求實數
上有兩個零點,求實數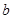 的取值范圍.
的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com